Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations trigonométriques
Solutions sur un un intervalle de R
Ressources associées et exercices semblables
Équations avec cosinus (réf 0727)
exercice
Équations avec sinus (réf 0728)
exercice
Fiche méthode résolution d’équations trigonométriques (réf 0754)
méthode
- Résoudre l'équation $cos(3x)=\dfrac{1}{2}$ dans $[0;2\pi[$
Rappel cours
Valeurs remarquables du cos et du sin
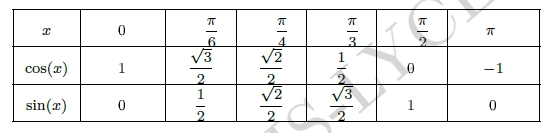
Aide
Déterminer les mesures principales $\alpha_1$ et $\alpha_2$ possibles pour $3x$
Résoudre les équations $3x=\alpha_1+k2\pi$ et $3x=\alpha_2+k2\pi$ avec $k\in \mathbb{Z}$
Déterminer les valeurs de $x$ appartenant à $[0;2\pi[$ pour les différentes valeurs de $k$ soit $k=0$, $k=1$, $k=-1$.....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre $sin(2x)=0$ sur $[-2\pi;2\pi]$
Aide
Chercher une mesure $\alpha$ telle que $sin(\alpha)=0$
En déduire les valeurs possibles $\alpha_1$ et $\alpha_2$ pour lesquelles $sin(\alpha_1)=0$ et $sin(\alpha_2)=0$
Résoudre les équations $2x=\alpha_1+k2\pi$ et $3x=\alpha_2+k2\pi$ avec $k\in \mathbb{Z}$
Déterminer les valeurs de $x$ appartenant à $[-2\pi;2\pi]$ pour les différentes valeurs de $k$ soit $k=0$, $k=1$, $k=-1$.....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre $cos(4x)=cos(\dfrac{\pi}{5})$ sur $[0;2\pi[$
Aide
Pour tout réel $x$, $cos(x)=cos(\pi-x)$
En déduire les valeurs possibles $\alpha_1$ et $\alpha_2$ pour lesquelles $cos(\alpha_1)=cos(\dfrac{\pi}{5}$ et $cos(\alpha_2)=cos(\dfrac{\pi}{5}$
Résoudre les équations $4x=\alpha_1+k2\pi$ et $4x=\alpha_2+k2\pi$ avec $k\in \mathbb{Z}$
Déterminer les valeurs de $x$ appartenant à $[0;2\pi[$ pour les différentes valeurs de $k$ soit $k=0$, $k=1$, $k=-1$.....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements