Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Se repérer sur le cercle trigonométrique
angles associés à π/4
cosinus et sinus des angles associés
Ressources associées et exercices semblables
Valeurs remarquables du cos et sin et angles associés (réf 0715)
exercice
Fiche méthode retrouver les valeurs du cosinus et sinus avec les angles associés (réf 0753)
Vidéo de l’exercice
- Rappeler la valeur exacte de $cos\left(\dfrac{\pi}{4}\right)$
Solution
- Sur le cercle trigonométrique, placer les points $A$, $B$, $C$ et $D$ associés aux réels $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$, $\dfrac{-3\pi}{4}$ et $\dfrac{-\pi}{4}$.
Aide
On peut convertir les mesures en degrés ou bien utliser les axes du repère
Solution
$\dfrac{\pi}{4}$ est la moitié de $\dfrac{\pi}{2} $
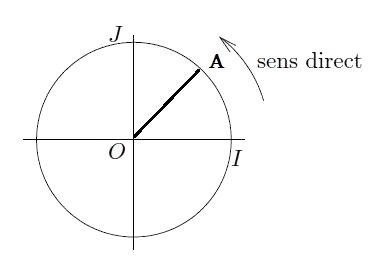
$\dfrac{3\pi}{4}=\pi-\dfrac{\pi}{4}$
donc $B$ est le symétrique de $A$ par rapport à l'axe des ordonnées.
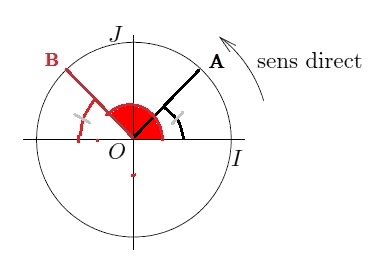
On a $\widehat{IOA}=\widehat{IOD}$ mais l'enroulement se fait dans le sens indirect pour le point $D$ (réel négatif)
De même $\widehat{IOB}=\widehat{IOC}$ mais l'enroulement se fait dans le sens indirect pour le point $C$ (réel négatif)
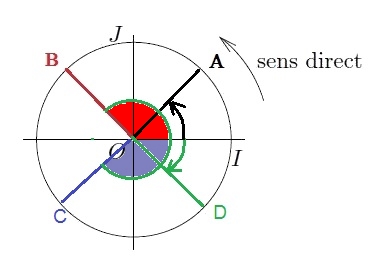
- En déduire les valeurs exactes du $cos$ et du $sin$ pour $\dfrac{\pi}{4}$, $\dfrac{3\pi}{4}$, $\dfrac{-3\pi}{4}$ et $\dfrac{-\pi}{4}$
Rappel cours
Valeurs remarquables du cos et du sin
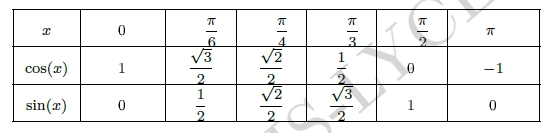
Aide
Utiliser les symétries effectuées à la question 1
Solution
Par symétrie on a $x_B=-x_A$ et $y_B=y_A$
Par symétrie on a $x_C=-x_B$ et $y_C=-y_B$
Par symétrie on a $x_D=x_A$ et $y_D=-y_A$