Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Notations des limites
Interprétation graphique des limites et asymptotes
Ressources associées et exercices semblables
Lecture graphique des limites et asymptotes (réf 0980)
exercice
Notations des limites et lecture d’un tableau de variation (réf 0982)
exercice
Vidéo de l’exercice
dans chaque cas, donner une représentation graphique possible de $f$ en traçant les asymptotes éventuelles.
- Cas 1:

Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
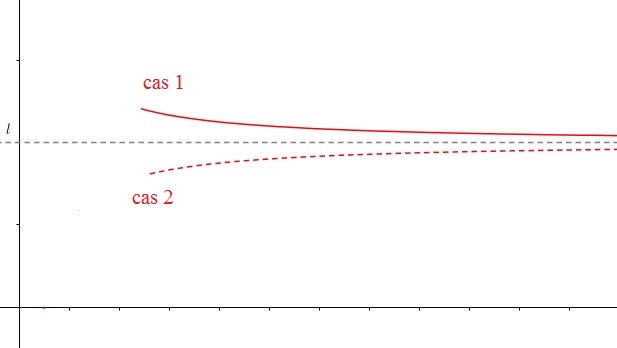
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$
Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.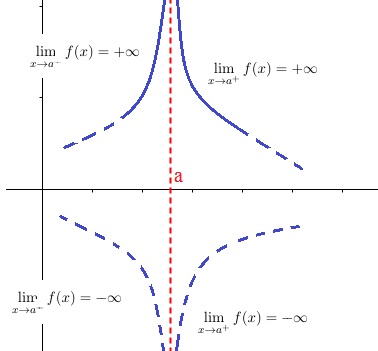
Aide
On doit tracer les droites d'équations $x=-3$ et $y=5$ (asymptotes)
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Cas 2:
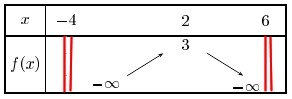
Aide
On doit tracer les droites d'équations $x=-4$ et $y=6$ (asymptotes)
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Cas 3:
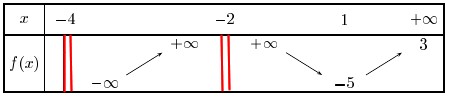
Aide
On doit tracer les droites d'équations $x=-4$ et $x=-2$ et $y=3$ (asymptotes)
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message