Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lien entre une primitive F et la fonction f
Identification de la courbe f connaissant F en utilisant les variations de F
Coefficient directeur d’une tangente
Ressources associées et exercices semblables
Identifier la courbe de f avec la courbe de F primitive de f (réf 1142)
exercice
Vidéo de l’exercice
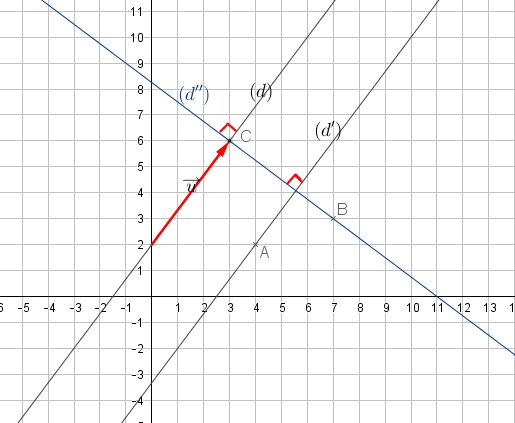
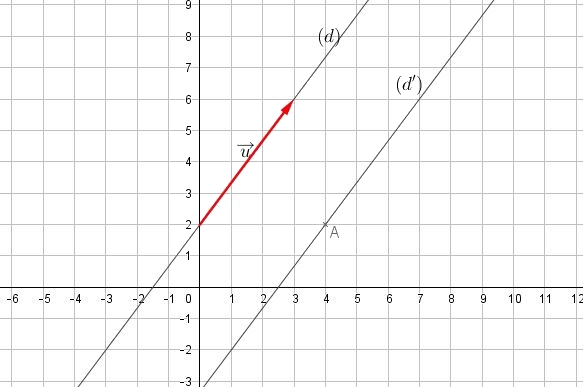
- Une des trois courbes ci-dessous est la représentation graphique de la fonction $f$ . Déterminer laquelle.
Rappel cours
Primitive d'une fonction
$F$ définie et dérivable sur $I$ est une primitive de $f$ sur $I$ si et seulement si $F'(x)=f(x)$.
Toute fonction $f$ continue sur $I$ admet des primitives.
Par exemple $F(x)=x^2$ définie et dérivable sur $\mathbb{R}$ est une primitive de $f(x)=2x$ sur $\mathbb{R}$Aide
Dresser le tableau de variation de la fonction $F$ en utilisant sa représentation graphique $C_F$
En déduire le signe de $f(x)$.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant le graphique, déterminer alors $f(0)$ et tracer la tangente à la courbe De $F$ au point d'abscisses $0$.
Rappel cours
Le coefficient directeur d'une tangente à la courbe de $f$ au point d'abscisse $a$ est $f'(a)$
Aide
$F'(0)=f(0)$ et est le coefficient directeur de la tangente à la courbe $F$ en $0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message