Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Primitives avec les fonctions usuelles (racine carrée, polynômes et inverse)
Ressources associées et exercices semblables
Primitives avec les fonctions usuelles (réf 1146)
exercice
Exercice | temps recommandé entre 5 et 10mn
| Niveau 2 difficulté moyenne
| séquence 2 du chapitre
|
Vidéo de l’exercice
Déterminer une primitive $F$ de $f$ dans chaque cas en précisant l'ensemble de définition.
- $f(x)=x^2-\dfrac{1}{x^3}$
Rappel cours
Primitives des fonctions usuelles
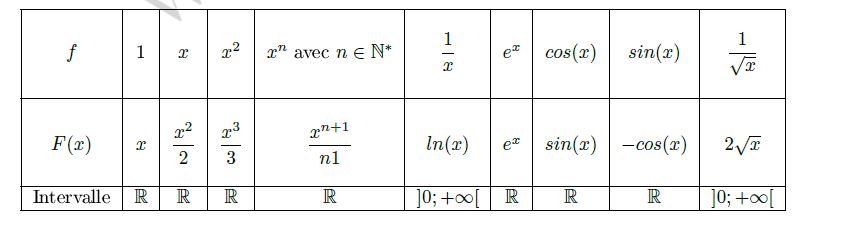
Aide
Il faut que $x^3\neq 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $f(x)=\dfrac{1}{\sqrt{x}}+x+2$
Aide
Il faut $x >0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $f(x)=\dfrac{3}{x}-6x^2+6x-1$
Aide
Attention Si $x\neq 0$ une primitive de $u(x)=\dfrac{1}{x}$ sur $\mathbb{R}^*$ est $U(x)=ln(|x|)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Vous devez être abonné pour accéder à ce contenu...