Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calculs de probabilités avec un arbre
Probabilités conditionnelles et totales
Ressources associées et exercices semblables
Extrait BAC calculs de probabilités avec un arbre (réf 1307)
exercice
Extrait BAC probabilités conditionnelles et totales (réf 1310)
exercice
La probabilité que l'événement $A$ soit réalisé est $0,3$.
La probabilité que l'événement $B$ soit réalisé sachant que $A$ est réalisé est $0,6$.
La probabilité que l'événement $B$ soit réalisé $0,53$.
- Traduire les données de l'énoncé avec les notations des probabilités et compléter l'arbre ci-dessous.
Rappel cours
Arbre pondéré
Probabilités sur un arbre pondéré:
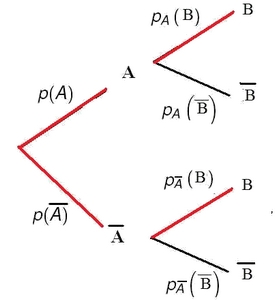
Aide
On ne peut compléter toutes les branches de l'arbre car $p(B)$ ne peut Être placée.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Calculer $p(A\cap B)$.
Rappel cours
include166flude
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - En utilisant la formule des probabilités totales, calculer $p(\overline{A}\cap B)$ puis $p_{\overline{A}}(B)$.
Rappel cours
Probabilités totales
Soient $A_1$, $A_2$,...$A_n$ des événements de l'univers $\Omega$ tels que $p(A_1)\neq 0$, $p(A_2)\neq 0$...$p(A_n)\neq 0$ et $B$ un événements.
Si $A_1$, $A_2$,...$A_n$ sont deux à deux disjoints et que leur réunion forme l'univers $\Omega$ alors $A_1$, $A_2$...$A_n$ forment une partition de $\Omega$
et on a $p(B)=p(A_1\cap B)+p(A_2\cap B)+...+p(A_n\cap B)$}
$A$ et $\overline{A}$ forment une partition de l'univers et on a $p(B)=p(A\cap B)+p(\overline{A}\cap B)$Aide
Ecrire la formule des probabilités totales pour $p(B)$ et remplacer les probabilités connues pour obtenir une équation d'inconnue $p(\overline{A}\cap B)$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Compléter alors l'arbre pondéré.
Rappel cours
Arbre pondéré
Probabilités sur un arbre pondéré:
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION