Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Affixe d’un point et d’un vecteur
Ressources associées et exercices semblables
QCM séquence 4 propriétés des modules et des arguments (réf 1449)
QCM
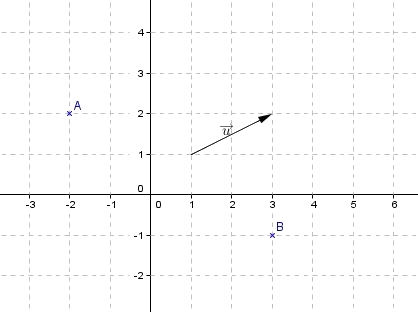
- Déterminer l'affixe de $A$, $B$ et $\overrightarrow{u}$ par lecture graphique.
Rappel cours
Affixe d'un point et d'un vecteur
Le complexe $z=x+iy$ ($x$ et $y$ réels) est l'affixe du point $M(x;y)$. %l Avec $\overrightarrow{u}\begin{pmatrix}a\\b\end{pmatrix}$, le complexe $u=a+ib$ est l'affixe du vecteur $\overrightarrow{u}$.Solution
Graphiquement on a $A(-2;2)$ donc $z_A=-2+2i$, $B(3;-1)$ donc $z_B=3-i$ et $\overrightarrow{u}(2;1)$ donc $z_{\overrightarrow{u}}=2+i$.
- Calculer l'affixe du vecteur $\overrightarrow{AB}$ et en déduire $AB$.
Aide
Il faut calculer $z_B-z_A$ puis |z_B-z_A|$
Solution
$z_{\overrightarrow{AB}}=z_B-z_A=3-i-(-2+2i)=3-i+2-2i=5-3i$
$AB=|z_{\overrightarrow{AB}}|=\sqrt{5^2+(-3)^2}=\sqrt{34}$
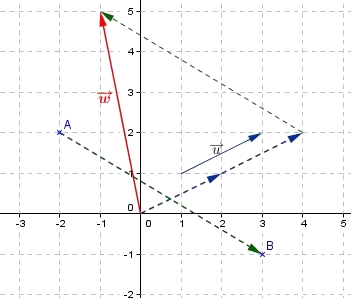
- Construire le vecteur $\overrightarrow{w}=2\overrightarrow{u}-\overrightarrow{AB}$ et calculer son affixe.
Contrôler graphiquement le résultat.Aide
Il faut calculer $2z_{\overrightarrow{u}}-z_{\overrightarrow{AB}}$
Solution
.
$z_{\overrightarrow{w}}=2z_{\overrightarrow{u}}-z_{\overrightarrow{AB}}$
$\phantom{z_{\overrightarrow{w}}}=2(2+i)-(5-3i)$
$\phantom{z_{\overrightarrow{w}}}=4+2i-5+3i$
$\phantom{z_{\overrightarrow{w}}}=-1+5i$
Graphiquement, on a bien $\overrightarrow{w}\begin{pmatrix}-1\\5\end{pmatrix}$


 Envoyez votre message
Envoyez votre message