Forme trigonométrique et exponentielle, équation de degré 2, ensemble de points (réf 1468) Chapitre 1 complexes, Option maths expertes, séquence 5 exercices de synthèse et devoirs d'entraînement

Déterminer l'écriture sous forme trigonométrique puis avec la notation exponentielle de $z$ et de $z'$

Rappel cours

Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$.
Valeurs remarquables du cos et du sin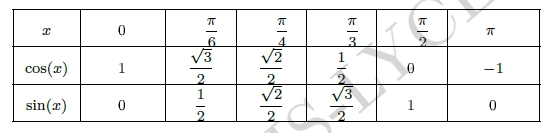

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire l'écriture exponentielle de $zz'$.

Rappel cours

Forme exponentielle
$z$ est un complexe d'argument $\alpha$
La forme exponentielle de $z$ est $z=|z|e^{i\alpha}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Calculer $zz'$ sous forme algébrique.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire la valeur exacte de $cos\left(\dfrac{\pi}{12}\right)$ et de $sin\left(\dfrac{\pi}{12}\right)$.

Aide

On peut utiliser l'écriture trigonométrique de $zz'$ et la forme algébrique de $zz'$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 2 (4 points)

Soit $z=-\sqrt{2+\sqrt{2}}+i\sqrt{2-\sqrt{2}}$.

Montrer que $z^2=2\sqrt{2}-2i\sqrt{2}$

Aide

On peut utiliser les identités remarquables avec $a=-\sqrt{2+\sqrt{2}}$ et $b=\sqrt{2-\sqrt{2}}$ et on a $a+b)^2=a^2+2ab+b^2$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer la forme exponentielle de $z^2$.

Rappel cours

Forme trigonométrique
Soit $z=x+iY$ un complexe.
Le module de $z$ noté $|z|$ est $|z|=OM=\sqrt{x^2+y^2}$.
Si $z\neq 0$ l'argument de $z$ noté $arg(z)$ est une mesure en radians de l'angle $(\overrightarrow{i};\overrightarrow{OM})$}
On a alors $x=|z|cos(arg(z))$ et $y=|z|sin(arg(z))$ soit $z=|z|(cos(arg(z)+isin(arg(z))$
Cette forme est appelée forme trigonométrique} de $z$. Valeurs remarquables du cos et du sin

Aide

Il faut calculer le module de $z^2$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire la forme exponentielle de $z$.

Aide

Si on note $\alpha=arg\left(z\right)$ ($2\pi$), on a $2\aplha=\theta+k2\pi$ avec $k\in \mathbb{Z}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire la forme algébrique de $z^{10}$.

Aide

Il faut utiliser la forme exponentielle de $z$ et déterminer la mesure principale de $\dfrac{70\pi}{8}$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 3 (4 points)

On considère le polynôme $P$ défini par $P(z) = z^4 - 6z^3 + 24z^2 - 18z + 63$.

Montrer qu'il existe 3 réels $a,b,c$ que l'on déterminera tels que $P(z)=(z^2 + 3)(az^2+bz+c)$.

Aide

Il faut développer $(z^2 + 3)(az^2+bz+c)$ et identifier les coefficients pour avoir $(z^2 + 3)(az^2+bz+c)= z^4 - 6z^3 + 24z^2 - 18z + 63$ pour tout complexe $z$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
En déduire les 4 racines complexes de $P$.

Rappel cours

Équations du second degré à coefficients réels
équation du second degré à coefficients réels
Discriminant: $\Delta=b^2-4ac$
- Si $\Delta \geq 0$, on résout dans $\mathbb{R}$
Si $\Delta >0 $ il y a 2 racines $z_1=\dfrac{-b-\sqrt{\Delta}}{2a}$ et $z_2=\dfrac{-b+\sqrt{\Delta}}{2a}$
Si $\Delta <0$ alors on a deux racines complexes conjuguées:
$z_1=\dfrac{-b-i\sqrt{|\Delta|}}{2a}$ et $z_2=\dfrac{-b+i\sqrt{|\Delta|}}{2a}=\overline{z_1}$

Aide

Il faut utiliser la forme factorisée de $P(z)$ et un produit de facteurs est nul si l'un des facteurs est nul

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 4 (6 points)

Le plan est muni d'un repère orthonormé et à tout point $M$ d'affixe $z\neq -i$ on associe le point $M'$ d'affixe $z'=\dfrac{z-2}{z+i}$.
On cherche l'ensemble $\mathcal{E}$ des points $M$ tels que $M'$ appartiennent à l'axe des ordonnées.
On note $A$ et $B$ les points d'affixes respectives $a=2$ et $b=-i$.

Méthode algébrique
1. On pose $z=x+iy$ avec $x$ et $y$ réels.
  Déterminer la partie réelle et imaginaire pure de $z'$ en fonction de $x$ et $y$.
  
  Rappel cours
  
  012 Suppression des complexes au dénominateur
  Pour écrire un nombre complexe sans complexes au dénominateur, il faut multiplier le numérateur et le dénominateur par le conjugué du dénominateur.
  En effet $(a+ib)(a-ib)=a^2-iab+iba-i^2b^2=a^2+b^2$
  soit $z\overline{z}=a^2+b^2$
  Exemple:
  $z=\dfrac{2+3i}{1-2i}=\dfrac{(2+3i)(1+2i)}{(1-2i)(1+2i)}=\dfrac{(2+3i)(1+2i)}{1+4}=\dfrac{(2+3i)(1+2i)}{5}$
  
  Aide
  
  012 Il faut multiplier le numérateur et le dénominateur de $z'$ par le conjugué de $x+iy+i$(dénominateur) soit $x-iy-i$
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements
2. En déduire que $\mathcal{E}$ est un cercle privé du point $B$ dont on précisera le centre et le rayon.
  
  Aide
  
  $M'$ appartient à l'axe des ordonnées si et seulement si $z'$ imaginaire pur si et seulement si $Re(z')=0$
  Rappel: le cercle de centre $C(x_C;y_C)$ et rayon $r$ a pour équation $(x-x_C)^2+(y-y_C)^2=r^2$
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements
Méthode géométrique
On note $M$ le point d'affixe $z$ avec $z\neq -i$.
1. Montrer que si $M\in \mathcal{E}$ alors on a $arg\left(\dfrac{z-a}{z-b}\right)=\dfrac{\pi}{2}+k\pi$ avec $k\in \mathbb{Z}$
  
  Aide
  
  L'argument d'un complexe imaginair pur est $\dfrac{\pi}{2}$ ($2\pi$) ou $-\dfrac{\pi}{2}$ ($2\pi$)
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements
2. Retrouver alors l'ensemble $\mathcal{E}$ en utilisant la question précédente.
  
  Aide
  
  Le cercle circonscrit à un triangle $ABM$ rectangle en $M$ est le cercle de diamètre $[AB]$.
  
  Solution
  
  Vous devez être abonné pour accéder à ce contenu...
  Infos abonnements

Vous devez être abonné pour accéder à ce contenu...

Infos abonnements

Forme trigonométrique et exponentielle, équation de degré 2, ensemble de points (réf 1468)

Informations

Contenu

Ressources associées et exercices semblables

Ajoutez MATHS-LYCE sur votre mobile Homescreen!