Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Matrice d’un graphe
Matrices et calculatrice
Nombre de chaînes de longueur n sur un graphe
Chaînes fermées
Ressources associées et exercices semblables
Matrice d’un graphe et nombre de chaînes de longueur 3 (réf 1653)
exercice
Matrice d’un graphe et nombre de chaînes de longueur 3 (réf 1654)
exercice
$\begin{pmatrix} 0&1&1&0&1&0\\ 1&0&1&1&1&1\\ 1&1&0&0&0&1\\ 0&1&0&0&0&0\\ 1&1&0&0&0&1\\ 0&1&1&0&1&0 \end{pmatrix}$
- Construire le graphe associé à cette matrice.
Rappel cours
Matrice associée à un graphe
La matrice associée à un graphe d'ordre $n$ dont les sommets sont numérotés de 1 à n est une matrice carrée de dimension $n$, où le terme à l'intersection de la iième ligne et de la jième colonne est nombre d'arêtes reliant i et j.
Cette matrice est appelée matrice d'adjacence du graphe.
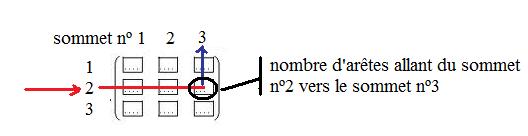
Aide
Le sommet numéro 1 est adjacent aux sommets 2, 3 et 5 (coefficients de la première ligne de la matrice)
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Avec la calculatrice, calculer $M^4$.
En déduire le nombre de chaînes de longueur 4 allant du sommet 2 au sommet 4.Rappel cours
Nombre de chemins de longueur $p$
Nombre de chaînes de longueur $p$}{Soit $G$ un graphe d'ordre $n$ et de matrice d'adjacence $M$.
Le coefficient $m_{ij}$ de la matrice $M^p$ ($p$ entier naturel non nul) est le nombre de chaînes de longueur $p$ reliant les sommets $i$ et $j$.}Aide
avec la calculatrice, saisir les coefficients de $M$ puis calculer $M^4$ (sur casio OPTN puis MAT puis MAT A$^4$, sur NumWorks, bo^te à outils puis matrices)
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements- A l'aide de la matrice, dire s'il existe une chaîne de longueur 3 reliant le sommet 1 au sommet 5.
Contrôler sur le graphe.Aide
Il faut calculer $M^3$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements- Existe-il des chaînes fermées de longueur $3$ partant du sommet 4? du sommet 5?
Rappel cours
Chaîne
Une chaîne est un liste ordonnée de sommets telle que chaque sommet de la liste soit adjacent au suivant.
La longueur d'une chaîne est le nombre d'arêtes qui la composent.
Si l'origine et l'extrémité de la chaîne sont identiques alors il s'agit d'une chaîne ferméeSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - A l'aide de la matrice, dire s'il existe une chaîne de longueur 3 reliant le sommet 1 au sommet 5.


 Envoyez votre message
Envoyez votre message