Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Utiliser les différentes expressions du produit scalaire
Développer et simplifier avec le produit scalaire
Ressources associées et exercices semblables
Calculs avec le produit scalaire (réf 0773)
exercice
Calcul du produit scalaire dans des triangles (réf 0798)
exercice
Aide mémoire complet produit scalaire et vecteurs (réf 0806)
mémo
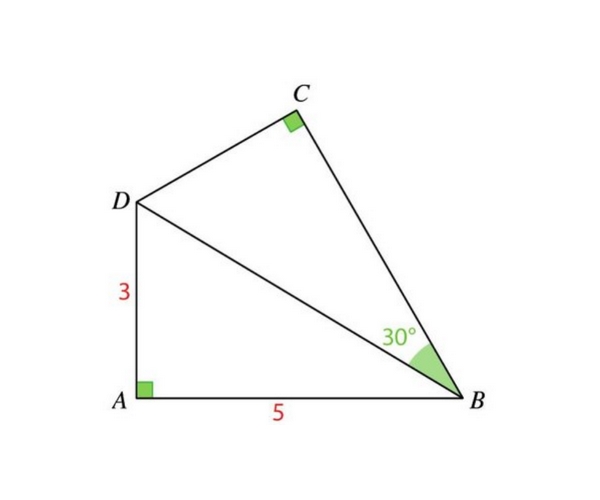
- $\overrightarrow{CB}.\overrightarrow{CD}$
Rappel cours
Orthogonalité
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$ non nuls, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.Aide
Les droites $(CB)$ et $(CD)$ sont orthogonales
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $\overrightarrow{BD}^2$
Rappel cours
Carré scalaire
$\overrightarrow{u}^2=\overrightarrow{u}.\overrightarrow{u}=||\overrightarrow{u}||^2$Aide
Il faut calculer la longueur $BD$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $\overrightarrow{DB}.\overrightarrow{AD}$
Rappel cours
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Aide
On peut utiliser $-\overrightarrow{DA}$ et le projeté orthogonal de $B$ sur $(AD)$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $\overrightarrow{BD}.\overrightarrow{BC}$
Rappel cours
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Aide
On peut utiliser le projeté orthogonal de $D$ ou bien l'angle $\overrightarrow{CBD}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $\overrightarrow{CD}^2$
Rappel cours
Carré scalaire
$\overrightarrow{u}^2=\overrightarrow{u}.\overrightarrow{u}=||\overrightarrow{u}||^2$Aide
Il faut calculer la longueur $CD$ dans $BCD$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $\overrightarrow{BC}.\overrightarrow{BA}$
Rappel cours
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Aide
On peut utiliser le projeté orthogonal de $D$ ou bien l'angle $\overrightarrow{CBD}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message