Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul d’un angle dans un triangle
Cos et sin dans le triangle rectangle
Calcul de la valeur exacte de cos(45) et sin(45)
Ressources associées et exercices semblables
- Calculer $\widehat{ABC}$ en radians et $AB$.
Aide
a somme des trois angles d'un triangle est de $\pi$ radians (soit 180 degrés) et un triangle isocèle a deux angles de même mesureSolution
$ABC$ est isocèle rectangle en $A$
donc $\widehat{BAC}=\dfrac{\pi}{2}$
et $\widehat{ABC}=\widehat{ACB}$.
$\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=\pi$ (somme des trois angles d'un triangle)
et comme $\widehat{ABC}=\widehat{ACB}$.
$\widehat{ABC}+\widehat{ABC}+\widehat{BAC}=\pi$
donc $2\widehat{ABC}+\dfrac{\pi}{2}=\pi$
soit $2\widehat{ABC}=\dfrac{\pi}{2}$
- Montrer que $AB=\dfrac{\sqrt{2}}{2}$.
Rappel cours
Théorème de Pythagore
Dans un triangle $ABC$ rectangle en $A$, on a $AB^2+AC^2=BC^2$Aide
On a $BC^2=1$ et $AB=AC$
Solution
$ABC$ est un triangle rectangle en $A$
$AB^2+AC^2=BC^2 \Longleftrightarrow 2AB^2=1$
$\phantom{AB^2+AC^2=BC^2} \Longleftrightarrow AB^2=\dfrac{1}{2}$
$\phantom{AB^2+AC^2=BC^2} \Longleftrightarrow AB=\sqrt{\dfrac{1}{2}}$
$\phantom{AB^2+AC^2=BC^2} \Longleftrightarrow AB=\dfrac{1}{\sqrt{2}}$
$\phantom{AB^2+AC^2=BC^2} \Longleftrightarrow AB=\dfrac{\sqrt{2}}{\sqrt{2}\sqrt{2}}$ (on multiplie le numérateur et le dénominateur par $\sqrt{2}$)
$\phantom{AB^2+AC^2=BC^2} \Longleftrightarrow AB=\dfrac{\sqrt{2}}{2}$
- En déduire la valeur exacte de $cos\left(\dfrac{\pi}{4}\right)$.
Rappel cours
Trigonométrie dans le triangle rectangle
$ABC$ est un triangle rectangle en $A$.
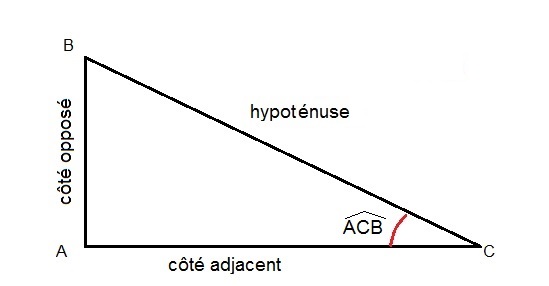
$cos(\widehat{ACB})=\dfrac{AC}{BC}=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}$
$sin(\widehat{ACB})=\dfrac{AB}{BC}=\dfrac{\text{côté opposé}}{\text{hypoténuse}}$
$tan(\widehat{ACB})=\dfrac{AB}{AC}=\dfrac{\text{côté opposé}}{\text{côté adjacent}}$
Aide
$cos(\widehat{ABC})=\dfrac{AB}{BC}$
Solution
$cos(\widehat{ABC})=\dfrac{AB}{BC}=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}$
soit $cos(\left(\dfrac{\pi}{4}\right)=\dfrac{\dfrac{\sqrt{2}}{2}}{1}=\dfrac{\sqrt{2}}{2}$
Remarque
$sin\left(\dfrac{\pi}{4}\right)=\dfrac{AC}{BC}=\dfrac{\text{côté opposé}}{\text{hypoténuse}}$
or $AC=AB$
donc $sin\left(\dfrac{\pi}{4}\right)=\dfrac{\sqrt{2}}{2}$


 Envoyez votre message
Envoyez votre message