Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Recherche du coût de production maximal
Maximum d’une fonction de polynôme de degré 2
Ressources associées et exercices semblables
Déterminer f (forme canonique) connaissant la parabole (réf 0489)
exercice
Déterminer la forme canonique à partir du graphique (réf 0458)
exercice
Vidéo de l’exercice
Déterminer l'expression de chacune de ces fonctions.
- Tableau 1:

La courbe représentative de $f$ coupe l'axe des ordonnées au point $A$ de coordonnées $(0;3)$.Rappel cours
Variations fonction polynôme du second degré
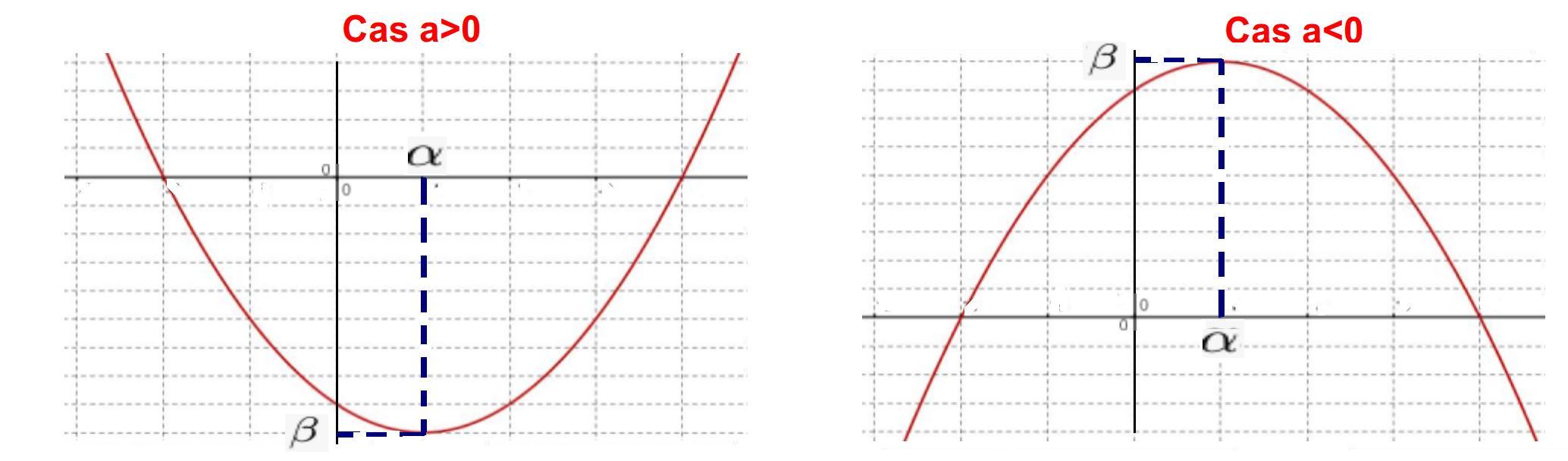
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: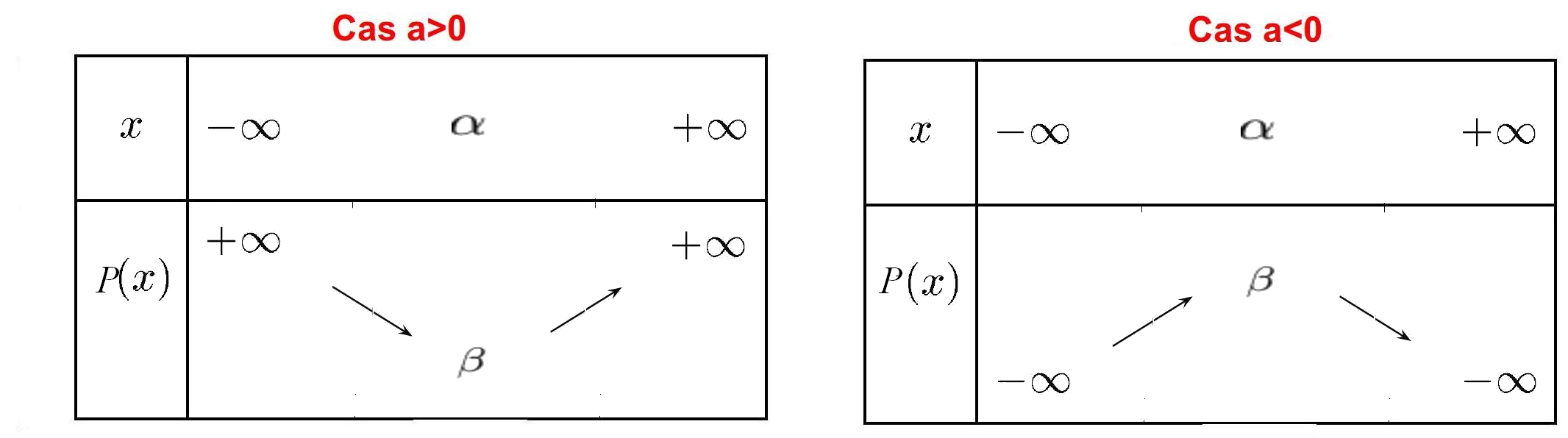
Aide
Déterminer les coordonnées du sommet de la parabole à laide du tableau de variation pour déterminer $\alpha$ et $\beta$ dans la forme canonique $f(x)=a(x-\alpha)^2+\beta$
On peut déterminer ensuite la valeur de $a$ en utilisant les coordonnées du point $A$ soit $f(0)=3$Solution
Vous devez être inscrit pour accéder à ce contenu, inscrivez-vous gratuitement!
- Tableau 2:

Le point $A$ de coordonnées $(4;16)$ appartient à la courbe représentative de $f$.Aide
Déterminer les coordonnées du sommet de la parabole à laide du tableau de variation pour déterminer $\alpha$ et $\beta$ dans la forme canonique $f(x)=a(x-\alpha)^2+\beta$
On peut déterminer ensuite la valeur de $a$ en utilisant les coordonnées du point $A(4;16)$ soit $f(4)=16$Solution
Vous devez être inscrit pour accéder à ce contenu, inscrivez-vous gratuitement!
- Tableau 3:

La courbe représentative de $f$ coupe l'axe des abscisses au point $A$ d'abscisse $2$.Solution
Vous devez être inscrit pour accéder à ce contenu, inscrivez-vous gratuitement!
- Tableau 2:


 Envoyez votre message
Envoyez votre message