Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Forme canonique
Racines et discriminant
Tableau de variation et courbe
Équations du second degré
Associer une fonction à sa représentation graphique
Ressources associées et exercices semblables
Méthode équations du second degré commentées (réf 0518)
méthode
- Déterminer la forme canonique de $f$.
Rappel cours
Forme canonique
Toute fonction polynôme de degré 2 définie sur $\mathbb{R}$ par $P (x) = ax^2 + bx + c$ peut s'écrire sous la forme $P (x) = a(x -\alpha)^2 + \beta$ avec $\alpha=\dfrac{-b}{2a}$ et $\beta= P ( \alpha)$.
Cette écriture de $P (x)$ est appelée forme canonique et $S(\alpha;\beta)$ est le sommet de la parabole représentant la fonction $P$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les solutions de l'équation $f(x)=0$.
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les coordonnées du point d'intersection de $C_f$ et de l'axe des ordonnées.
Aide
Le point d'intersection avec l'axe des ordonnées a pour abscisse $x=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de variation de $f$ puis donner l'allure de $C_f$ en mettant en évidence les résultats des questions précédentes dans le repère donné en annexe ex 1.
Rappel cours
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: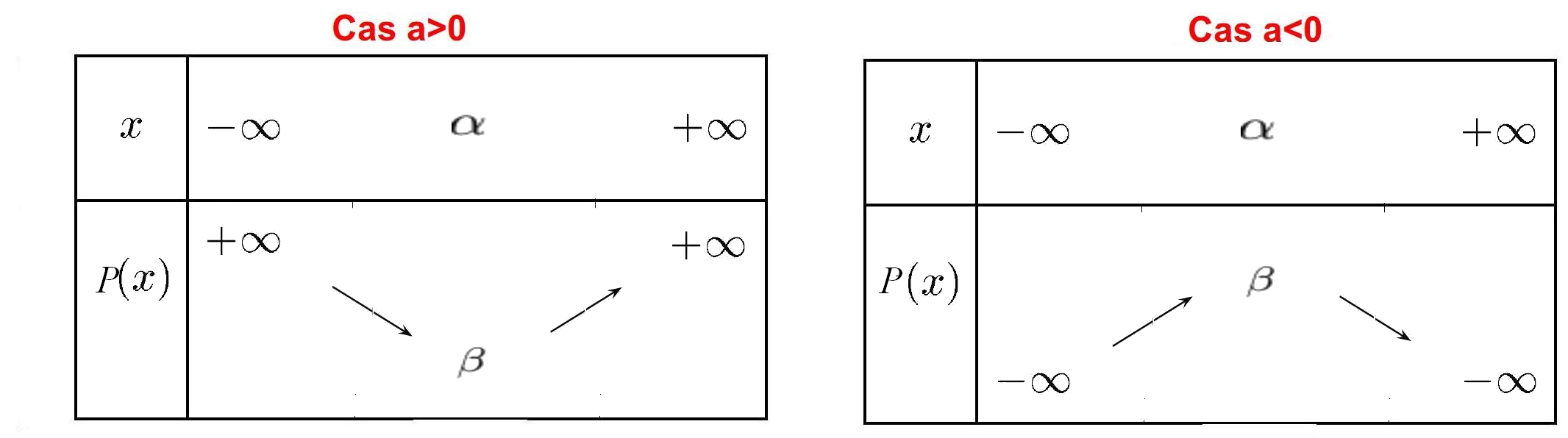
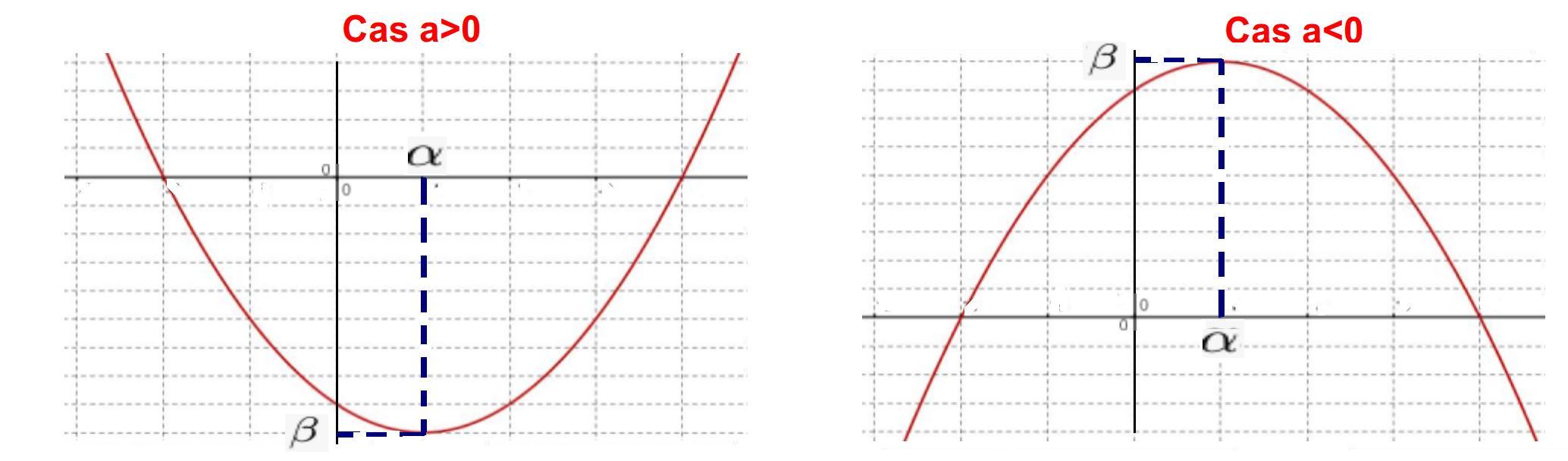
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- $4x^2-9=0$
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $2x^2-7x=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $2004x^2+1-2005=0$
Rappel cours
Somme et produit des racines
Si le polynôme $P(x)=ax^2+bx+c$ (avec $a\neq 0$) admet deux racines $x_1$ et $x_2$ alors on a:
$ x_1+x_2=\dfrac{-b}{a}$ (somme des racines)
et $x_1x_2=\dfrac{c}{a}$ (produit des racines)Aide
On peut vérifier que $x=1$ est une solution
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $-\dfrac{3}{4}x^2+2x-5 = 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $\dfrac{3x^2+10x+8}{x+2}=2x+5$
Aide
Il faut d'abord chercher la valeur interdite
On peut utiliser les produits en croixSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
$f(x)=-\frac{1}{2}x^2+x-1$
$g(x)=\frac{1}{4}x^2-2x-1$
$h(x)=-\frac{1}{3}x^2-2x-1$
$k(x)=\frac{1}{4}x^2+x-1$
Les représentations graphiques de ces quatre fonctions sont données en annexe ex 3 ci-dessous.
Annexe ex 3

Pour chacune de ces fonctions, indiquer laquelle des paraboles ci-dessous la représente, en justifiant.
Résoudre graphiquement l'inéquation $f(x)>g(x)$ en justifiant la réponse.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Annexe ex 1 (question 4)



 Envoyez votre message
Envoyez votre message