Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations et inéquations avec exponentielle
Calculs de dérivées avec exponentielle
Étude de fonction avec exponentielles
Ressources associées et exercices semblables
Interrogation calculs avec exponentielle et dérivées avec exponentielle (réf 0695)
devoir
- Résoudre dans $\mathbb{R}$ l'inéquation $e^{-2x-1}>1$
Rappel cours
Égalité et inégalités avec exponentielle
Pour tous réels $a$ et $b$, on a:
$e^a=e^b\Longleftrightarrow a=b$
$e^a < e^b\Longleftrightarrow a < b$
Aide
Remplacer 1 par $e^0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre dans $\mathbb{R}$ l'équation $e^{x^2}=e^{-3x+2}$
Rappel cours
Racines
Les racines de $p(x)=ax^2+bx+c$ avec$a\neq 0$ sont les valeurs de $x$ annulant $P$
c'est à dire telles que $P(x)=0$.
$\Delta=b^2-4ac$
Si $\Delta>0$ donc il y a deux racine $x_1=\dfrac{-b+\sqrt{\Delta}}{2a}$ et $x_2=\dfrac{-b-\sqrt{\Delta}}{2a}$
Si $\Delta=0$ il y a une racine (double) $x_1=\dfrac{-b}{2a}$
Si $\Delta<0$ il n'y a aucune racine
Remarque: Graphiquement, les racines sont les abscisses des points d'intersection de la parabole et de l'axe des abscisses.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre dans $\mathbb{R}$ l'équation $-2X^2-3X+5=0$
En déduire les solutions de l'équation $-2e^{2x}-3e^x+5=0$Aide
Poser $X=e^x$ et on a alors $e^{2x}=(e^x)^2=X^2$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
La tangente $\mathcal{T}$ à la courbe $\mathcal{C}$ au point A$(0~;-4)$ passe par le point B$(2~;~- 6)$.
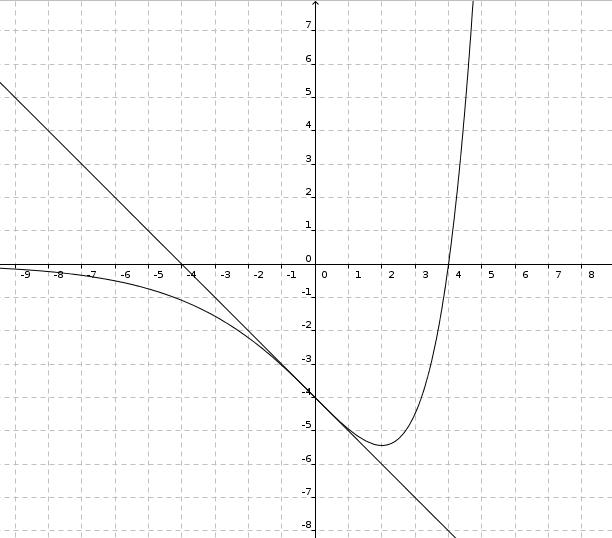
Partie A
On désigne par $f~'$ la fonction dérivée de $f$.
-
- Donner la valeur de $f(0)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Justifier que : $f~'(0) = - 1$.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Aide
Il faut déterminer le coefficient directeur de la tangente au point d'abscisse 0
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Donner la valeur de $f(0)$.
-
- On admet qu'il existe deux réels $a$ et $b$ tels que, pour tout réel $x$, $f(x) = (x + a)\text{e}^{bx}$.
Vérifier que pour tout réel $x$, $f~'(x) = (bx + ab + 1)\text{e}^{bx}$.Aide
On pose $u(x)=x+a $ et $v(x)=e^{bx} $
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Utiliser les résultats précédents pour déterminer les valeurs exactes des réels $a$ et $b$.
Aide
Ecrire deux équations d'inconnues $a$ et $b$ sachant que $f(0)=-4$ et que $f~'(0)=-1$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- On admet qu'il existe deux réels $a$ et $b$ tels que, pour tout réel $x$, $f(x) = (x + a)\text{e}^{bx}$.
On considère maintenant la fonction $f$ définie pour tout réel $x$ par $f(x) = (x - 4)e^{0,5x}$.
- Donner l'expression de $f~'(x)$ pour tout réel $x$ ; en déduire le sens de variation de la fonction $f$ sur l'ensemble des réels $\mathbb{R}$.
Rappel cours
Signe de exp(x)
Pour tout réel $x$ on a $e^x>0$Aide
Utiliser l'expression de $f~'(x)$ et $a=-4$ et $b=0,5$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On considère la fonction $g$ définie pour tout réel $x$ par $g(x)=f(x)+x+4$. On admet que la fonction $g$ est strictement croissante sur $\mathbb{R}$.
- Calculer $g(0)$ et en déduire le signe de $g(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer l'équation réduite de la tangente $T$ à la courbe $\mathcal{C}$ au point d'abscisse $0$ par le calcul.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Aide
Calculer $f(0)$ et $f'(0)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la position de la courbe $\mathcal{C}$ par rapport à sa tangente $\mathcal{T}$
Aide
Il faut étudier le signe de $f(x)-(-x+4)$
Utiliser le résultat concernant le signe de g(x)Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Calculer $g(0)$ et en déduire le signe de $g(x)$


 Envoyez votre message
Envoyez votre message