Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul de la valeur exacte de cos et sin π/8
Cosinus et sinus des angles associés à π/8 sur le cercle trigonométrique
Ressources associées et exercices semblables

- Calculer les coordonnées du point $A$ puis la distance $IA$.
Rappel cours
Trigonométrie dans le triangle rectangle
$ABC$ est un triangle rectangle en $A$.
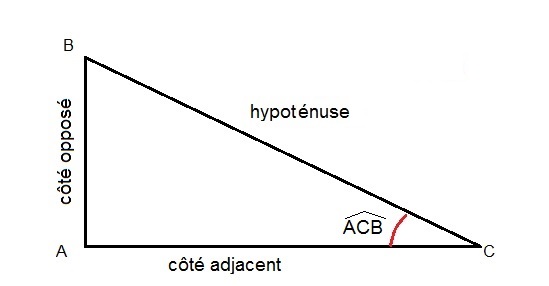
$cos(\widehat{ACB})=\dfrac{AC}{BC}=\dfrac{\text{côté adjacent}}{\text{hypoténuse}}$
$sin(\widehat{ACB})=\dfrac{AB}{BC}=\dfrac{\text{côté opposé}}{\text{hypoténuse}}$
$tan(\widehat{ACB})=\dfrac{AB}{AC}=\dfrac{\text{côté opposé}}{\text{côté adjacent}}$
 Distance dans un repère
Distance dans un repère
Dans un repère orthonormé du plan, on a $A(x_A;y_A)$ et $B(x_B;y_B)$,
$AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2}$
Si $\overrightarrow{u}(x;y)$ alors $||\overrightarrow{u}||=\sqrt{x^2+y^2}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les coordonnées de $H$ et en déduire la valeur exacte de $cos(\dfrac{\pi}{8})$ et de $sin(\dfrac{\pi}{8})$
Aide
Le triangle OIA est isocèle en O donc la hauteur issue de O est confondue avec la bissectrice de l'angle $\widehat{IOA}$
Le triangle IOH est un triangle rectangle en H.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire $cos(\dfrac{3\pi}{8})$
Rappel cours
Angles associés
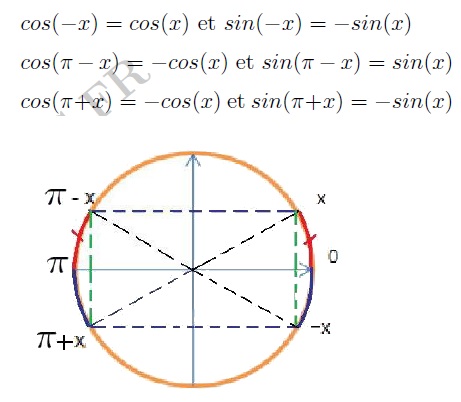
Aide
$\dfrac{\pi}{2}-\dfrac{\pi}{8}=\dfrac{3\pi}{8}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message