Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Justifier que f est dérivable en un point et calculer le nombre dérivé avec le taux d’accroissement
Déterminer l’équation réduite d’une tangente
Tracer une tangente à la courbe
Ressources associées et exercices semblables
Lecture graphique du nombre dérivé, équation et tracé d’une tangente (réf 0530)
exercice
On donne ci-dessous la représentation graphique $C_f$ de la fonction $f$ dans un repère orthogonal.
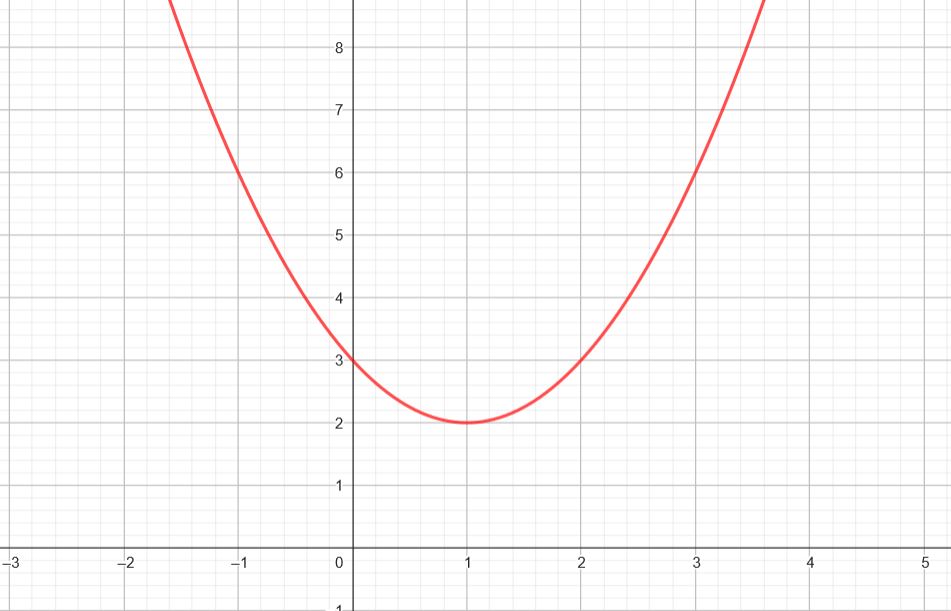
- En utilisant le taux d'accroissement, justifier que $f$ est dérivable en $x=2$ et donner la valeur de $f'(2)$.
Rappel cours
Nombre dérivé
Soit $f$ une fonction définie sur $D_f$ et $a$ appartenant à $D_f$.
S'il existe un réel $k$ tel que le taux d'accroissement $\dfrac{f(a+h)-f(a)}{h}$ de $f$ entre $a$ et $a+h$ se " rapproche" de $k$ lorsque $h$ se rapproche de 0 alors $f$ est dérivable en $x=a$.
$k$ est le nombre dérivé de $f$ en $x=a$ et se note $f'(a)$}$=k$.
On note alors $f'(a)=\displaystyle \lim_{h \rightarrow 0} \dfrac{f(a+h)-f(a)}{h}$ (se lit limite de $\dfrac{f(a+h)-f(a)}{h}$ quand $h$ tend vers 0.)
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une équation de la tangente à la courbe en $x=2$ et la tracer.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que $f'(1)=0$ et tracer la tangente $T'$ au point d'abscisse $1$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La droite $T''$ d'équation $y=-4x+2$ est la tangente à la courbe au point d'abscisse $-1$.
Quelle est la valeur de $f'(-1)$?
Tracer cette tangente.Aide
$f'(a)$ est le coefficient directeur de la tangente au point d'abscisse $a$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message