Lecture graphique du nombre dérivé et équation d’une tangente (réf 0555) Chapitre 2 dérivation, PREMIÈRE SPÉCIALITÉ MATHS, séquence 4 exemples d'études de variations

Home PREMIÈRE SPÉCIALITÉ MATHS Chapitre 2 dérivation séquence 4 exemples d'études de variations

Lecture graphique du nombre dérivé et équation d’une tangente (réf 0555)

Ressource précédente: Identifier la courbe de la dérivée avec les variations de f (réf 0554) Ressource suivante: Exercice de synthèse chapitre dérivation (réf 0571)

Infos

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Coefficient directeur d’une tangente

Lecture graphique du nombre dérivé

Équation réduite d’une tangente

Ressources associées et exercices semblables

Fiche méthode tangentes à une courbe (réf 0577)
méthode

| | | |

On donne ci-dessous sa représentation graphique dans un repère orthogonal.
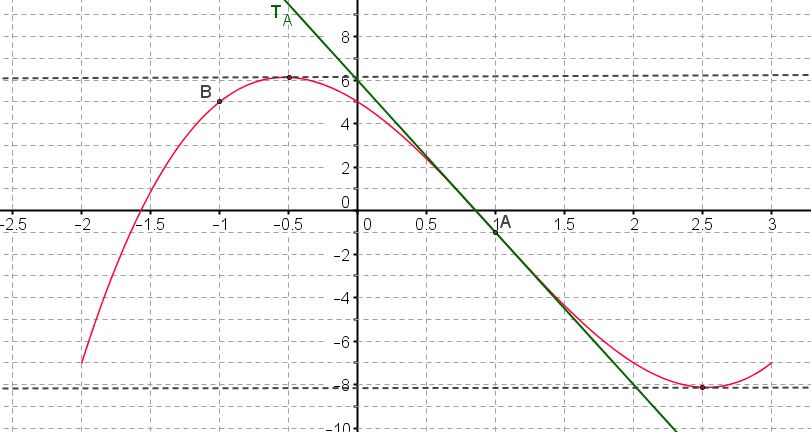
coefficient directeur d'une tangente et nombre dérivé

La droite $T_A$ est la tangente à la courbe au point $A$ d'abscisse 1.
Les tangentes aux points d'abscisses $-0,5$ et 2,5 sont parallèles à l'axe des abscisses.

A laide du graphique et des informations données dans l'énoncé, déterminer:
1. $f~'(2,5)$ et $f~'(-0,5)$
  
  Rappel cours
  
  Équation de la tangente au point d'abscisse $a$
  $f$ est une fonction définie et dérivable en $x=a$.
  La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
  et pour équation réduite $ y=f'(a)(x-a)+f(a)$}
  
  Aide
  
  Le coefficient directeur d'une droite parallèle à l'axe des abscisses est nul
  
  Solution
  
  Vous devez être inscrit pour accéder à ce contenu gratuitement!
  INSCRIPTION
2. $f~'(1)$
  
  Solution
  
  Vous devez être inscrit pour accéder à ce contenu gratuitement!
  INSCRIPTION
3. le signe de $f~'(-1)$
  
  Rappel cours
  
  Signe de la dérivée et variations d'une fonction
  Soit $f$ une fonction définie et dérivable sur $I$:
  $f$ est croissante sur $I$ si et seulement si $f'(x)\geq 0$
  $f$ est décroissante sur $I$ si et seulement si $f'(x)\leq 0$
  
  Aide
  
  Il faut déterminer le sens de variation de $f$ sur un intervalle contenant $-1$
  
  Solution
  
  Vous devez être inscrit pour accéder à ce contenu gratuitement!
  INSCRIPTION
On donne $f~'(-1)=5$.
Déterminer l'équation réduite de la tangente $T_B$ à la courbe au point $B$ d'abscisse $-1$.

Rappel cours

Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}

Aide

On donne $f~'(-1)$ et il faut déterminer graphiquement $f(-1)$

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Dresser le tableau de signes de $f~'(x)$

Rappel cours

Signe de la dérivée et variations d'une fonction
Soit $f$ une fonction définie et dérivable sur $I$:
$f$ est croissante sur $I$ si et seulement si $f'(x)\geq 0$
$f$ est décroissante sur $I$ si et seulement si $f'(x)\leq 0$

Aide

Il faut déterminer le sens de variation de $f$ pour connaître le signe de sa dérivée

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION

Inscrivez-vous pour accéder à ce contenu gratuitement!

INSCRIPTION

Ressource précédente: Identifier la courbe de la dérivée avec les variations de f (réf 0554) Ressource suivante: Exercice de synthèse chapitre dérivation (réf 0571)