Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Inscrivez vous gratuitement ici....
Contenu
Identifier la parabole associée à un polynôme de degré 2
Signe de a et orientation de la parabole
Ressources associées et exercices semblables
Déterminer la forme canonique à partir du graphique (réf 0458)
exercice
Méthode recherche de l’expression de f connaissant la parabole (réf 0517)
méthode
- Déterminer la représentation graphique de chacune des fonctions ci-dessous définies sur $\mathbb{R}$.
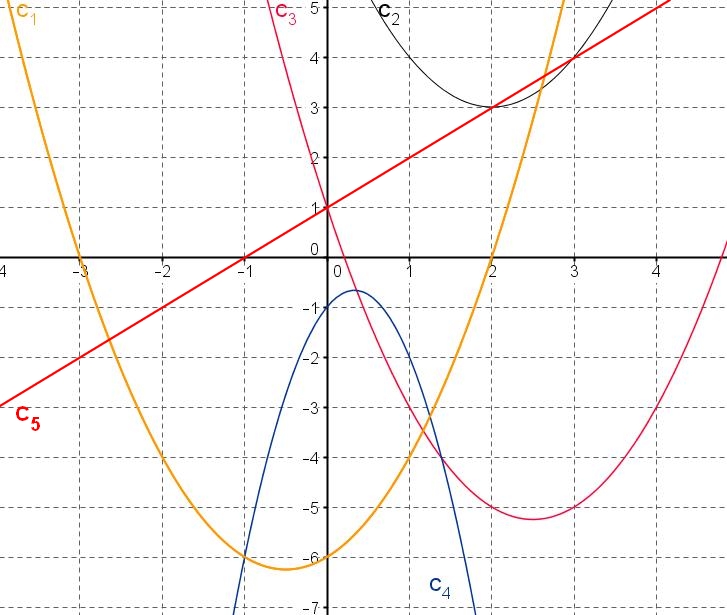
$f(x)=x^2-5x+1$, $g(x)=-3x^2+2x-1$, $h(x)=(x-2)^2+3$, $i(x)=(x-2)(x+3)$ et $j(x)x+1$
Rappel cours
Parabole
La représentation graphique d'une fonction polynôme de degré 2 est une parabole.
$S$ est le sommet de la parabole.
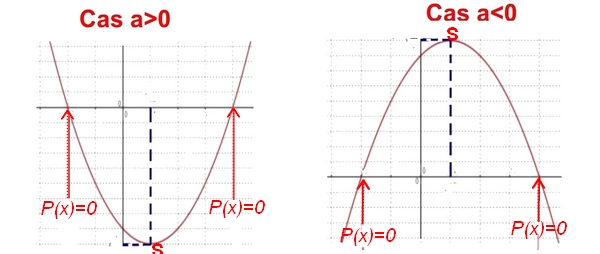
Si $P(x)=ax^2+bx+c$ on a:
 Fonction polynôme du second degré
Fonction polynôme du second degré
Une fonction $P$ définie sur $\mathbb{R}$ est une fonction polynôme de degré 2 s'il existe trois réels $a$, $b$ et $c$ avec $a\neq 0$ tels que pour tout réel $x$, $P (x) = ax^2 + bx + c$Aide
On peut calculer l'image de 0 par exemple pour déterminer les coordonnées d'un point de chacune des courbes représentatives.
On peut aussi utiliser le signe du coefficient $a$ de $x^2$Solution
Le seul coefficient de $x^2$ négatif est celui de la fonction $g$
La fonction $j$ est de la forme $j(x)=ax+b$ est donc une fonction affine
donc sa représentation graphique est une droite.
$f$ est une fonction polynôme de degré 2 (forme $ax^2+bx+c$ avec $a=1$
et $f(0)=0^2-5\times 0+1=1$
donc la courbe représentative de $f$ passe par le point de coordonnées $(0;1)$
.
$h(x)=(x-2)^2+3=x^2-4x+4+3=x^2-4x+7$
donc $h$ est une fonction polynôme de degré 2 (forme $ax^2+bx+c$ avec $a=1$
et $h(1)=(1-2)^2+3=1+3=4$
donc la courbe représentative de $h$ passe par le point de coordonnées $(1;4)$
.
$i(x)=(x-2)(x+3)$
$~~~~=x^2-2x+3x-6$
$~~~~=x^2+x-6$
donc $i$ est une fonction polynôme de degré 2 (forme $ax^2+bx+c$ avec $a=1$
et $i(0)=(0-2)(0+3)=-6$
donc la courbe représentative de $i$ passe par le point de coordonnées $(0;-6)$
. - En déduire graphiquement les solutions de l'équation $i(x)=0$ puis de $j(x)=0$
Aide
Graphiquement, les solutions de l'équation $i(x)=0$ sont les abscisses des points d'intersection de la courbe et de l'axe des abscisses.
Solution
Graphiquement, les solution de l'équation $i(x)=0$sont les abscisses des points d'intersection de la courbe $C_1$ et de l'axe des abscisses
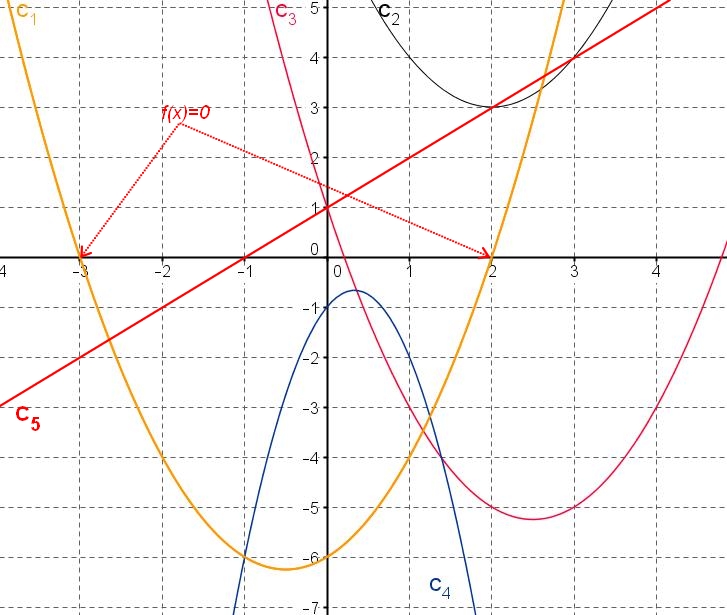
donc $i(x)=0$ pour $x=-3$ et pour $x=2$
$i(x)=0 $ pour $x=-1$


 Envoyez votre message
Envoyez votre message