Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Volume d’un parallélépipède rectangle
Dérivée d’un polynôme
Factorisation d’un polynôme de degré 3
Signe de la dérivée, tableau de variation et recherche d’un minimum
Ressources associées et exercices semblables
Quelles sont les dimensions du réservoir si on veut utiliser le moins de tôle possible?
Etape 1:
Aide
Rappel: 1 litre=1dm$^3$
La base est carrée donc les dimensions du réservoir peuvent être notées $x$ et $h$ (largeur $x$ mètres, longueur $x$ mètres et hauteur $h$ mètres.
Le volume d'un parallélépipède rectangle de dimensions $L$, $l$ et hauteur $h$ est $V=L\times l\times h$
L'aire totale de tôle utilisée est égale à l'aire totale des 6 faces du parallélépipède rectangle
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Etape 2:
Aide
Le volume est de 1m$^3$
Exprimer alors $h$ en fonction de $x$
En déduire alors l'expression de l'aire totale des faces en fonction de $x$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Etape 3:
Rappel cours
Dérivées usuelles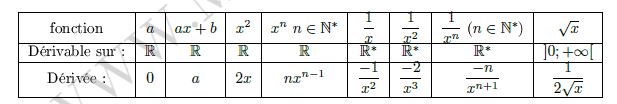
Aide
On pose $f(x)=2x²+\dfrac{4}{x}$ avec $x>0$
Calculer $f'(x)$ puis étudier les variations de $f$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Etape 4:
Méthode 1:
Aide
$x^3-1$ est un polynôme de degré 3,il faut chercher une racine puis factoriser pour étudier son signe.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Méthode 2:
Aide
On peut étudier les variations de la fonction auxiliaire $g$ définie sur $]0;+\infty[$ par $g(x)=x^3-1$
En utilisant les variations de $g$ et le fait que $g(1)=0$, on peut en déduire ñe signe de $g(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Conclusion:
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message