Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul du produit scalaire avec les normes des vecteurs et l’angle
Ressources associées et exercices semblables
Utiliser la bonne expression du produit scalaire (réf 0762)
exercice
Utiliser la bonne expression du produit scalaire (réf 0763)
exercice
Aide mémoire les différentes expressions du produit scalaire (réf 0805)
mémo
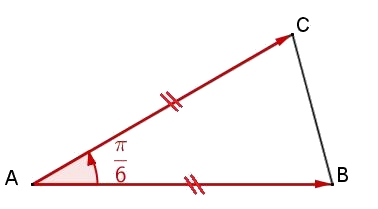
- $ABC$ est un triangle isocèle en A tel que $AB=5cm$ et $\widehat{BAC}=30^o$.
Calculer $ \overrightarrow{AB}$ et $ \overrightarrow{AC}$.Rappel cours
Produit scalaire (définition)
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$Aide
utiliser l'angle $\widehat{BAC}$
Solution
30$^o$ correspondent à $\dfrac{\pi}{6}$ radians et $cos(\dfrac{\pi}{6})=\dfrac{\sqrt{3}}{2}$
$ \overrightarrow{AB}. \overrightarrow{AC}=|| \overrightarrow{AB}||\times || \overrightarrow{AC}||\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=AB \times AC\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=5\times 5\times \dfrac{\sqrt{3}}{2}$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=\dfrac{25\sqrt{3}}{2}$
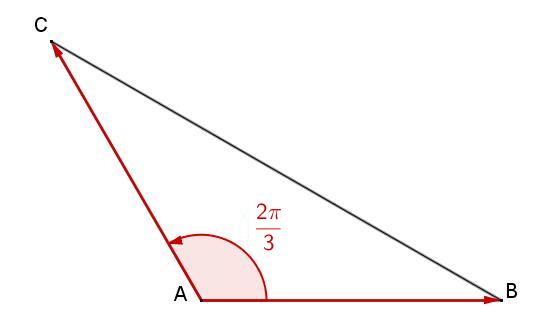
- $ABC$ est un triangle isocèle en A tel que $AB=5cm$ et $\widehat{BAC}=120^o$.
Calculer $ \overrightarrow{AB}$ et $ \overrightarrow{AC}$Rappel cours
Valeurs remarquables du cos et du sin
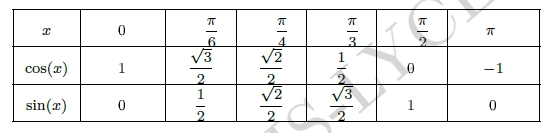
Aide
$\dfrac{2\pi}{3}=\pi-\dfrac{\pi}{3}$
Solution
120$^o$ correspondent à $\dfrac{2\pi}{3}$ radians ($2\times 180 \div 3=120$)
$\dfrac{2\pi}{3}=\pi-\dfrac{\pi}{3}$
et $cos(\dfrac{2\pi}{3})=-cos(\dfrac{\pi}{3})=-\dfrac{1}{2}$
$ \overrightarrow{AB}. \overrightarrow{AC}=|| \overrightarrow{AB}||\times || \overrightarrow{AC}||\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=AB \times AC\times cos( \overrightarrow{AB}, \overrightarrow{AC})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=5\times 5\times (-\dfrac{1}{2})$
$\phantom{ \overrightarrow{AB}. \overrightarrow{AC}}=-\dfrac{25}{2}$


 Envoyez votre message
Envoyez votre message