Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calcul du produit scalaire dans un carré en utilisant l’angle ou le projeté orthogonal
Ressources associées et exercices semblables
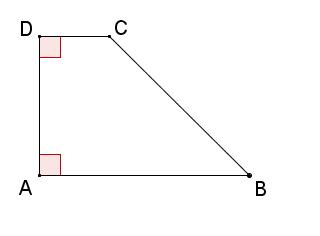
- Calculer $ \overrightarrow{AB}. \overrightarrow{CD}$.
Rappel cours
Produit scalaire (définition)
$\overrightarrow{u}$ et $\overrightarrow{v}$ sont deux vecteurs non nuls tels que $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$, le produit scalaire des deux vecteurs est noté $\overrightarrow{u}.\overrightarrow{v}$,et est le nombre réel défini par:
$\overrightarrow{u}.\overrightarrow{v}=\mid \mid \overrightarrow{u}\mid \mid\times \mid \mid \overrightarrow{v}\mid \mid \times cos(\widehat{BAC})=AB\times AC\times cos(\widehat{BAC})$Aide
On peut construire $B'$ tel que $\overrightarrow{CB'}=\overrightarrow{CB}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Calculer $ \overrightarrow{BA}. \overrightarrow{BC}$.
Rappel cours
Produit scalaire et projeté orthogonal
Soit $A$, $B$ et $C$ trois points ($A$ et $B$ distincts) et $\overrightarrow{u}=\overrightarrow{AB}$ et $\overrightarrow{v}=\overrightarrow{AC}$.
Si $H$ est le projeté orthogonal de $C$ sur $(AB)$:
$\overrightarrow{u}.\overrightarrow{v}=AB\times AH$ si $\widehat{BAH}=0$ (soit $\widehat{BAC}$ aigu)
et $\overrightarrow{u}.\overrightarrow{v}=-AB\times AH$ si $\widehat{BAH}=\pi$ (soit $\widehat{BAC}$ obtus)Aide
Soit $H$ le projeté orthogonal de $C$ sur $(AB)$, déterminer la nature du triangle $BHC$
Utiliser le point $H$ et les distances $BA$ et $BH$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Calculer $ \overrightarrow{AD}. \overrightarrow{CB}$.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message