Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Suites arithmétiques
Suites géométriques et suites arithmético-géométriques
Ressources associées et exercices semblables
Interrogation suites arithmétiques et géométriques (réf 0644)
devoir
- Etudier le sens de variation de la suite $(u_n)$ définie par $u_0= \dfrac{1}{2}$ et $u_{n+1}=u_n^2+2$ pour tout $n \in \mathbb{N}$.
Rappel cours
Étude des variations(différence de deux termes consécutifs)
Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
Exprimer $u_{n+1}-u_n$ en fonction de $n$
Étudier le signe de l'expression obtenue
Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante.
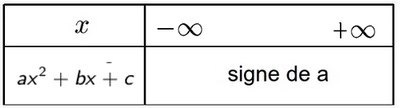
Signe de $ax^2+bx+c$
- Cas $\Delta>0$ (deux racines $x_1$ et $x_2$

- Cas $\Delta=0$ (une racine $x_1$)
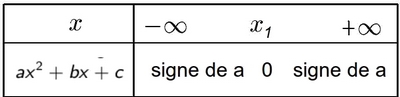
- Cas $\Delta<0$ (aucune racine)
Aide
On peut calculer $u_{n+1}-u_n$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $(u_n)$ est une suite géométrique de raison $q > 0$ telle que $u_5=16$ et $u_7=256$ : calculer $q$, $u_0$ puis donner la forme explicite de la suite $(u_n)$.
Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Aide
On peut écrire une équation d'inconnue $q$ en utilisant $u_5$ et $u_7$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Cela signifie que les prix augmentent en moyenne de 2% chaque année.
On note $p_n$ le prix d'un produit en $2012+n$ avec $n\in \mathbb{N}$.
En 2012, le prix de ce produit est de 20 euros.
- Que représente $p_0$? Donner sa valeur.
Aide
$p_0$ correspond au prix de l'année $2012+0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la nature de la suite $(p_n)$ en justifiant la réponse.
Rappel cours
Coefficient multiplicateur
Une quantité $V_i$ à laquelle on applique un taux d'évolution $t$ est multipliée par $k=1+t$.
Rappel: $t=\dfrac{V_f-V_i}{V_i}$
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Aide
augmenter une valeur de 2% revient à appliquer le coefficient multiplicateur $1+\dfrac{2}{100}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer le prix du produit en 2020.
Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Aide
déterminer d'abord la forme explicite de $(p_n)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer à partir de quelle année le prix aura augmenté de 50%.
Aide
On veut que le prix $p_n$ soit supérieur ou égal à 20 euros augmenté de 50% soit 30 euros
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère la suite $\left(u_{n}\right)$ définie par $u_{1} = 30$ et pour tout entier naturel $n\geq 1$, $u_{n+1} = 1,1u_{n} -2$.
On considère la suite $\left(v_{n}\right)$ définie pour tout entier naturel $n$ par $v_{n} = u_{n} - 20$.
- Démontrer que la suite $\left(v_{n}\right)$ est une suite géométrique dont on précisera le premier terme et la raison.
Rappel cours
Suite géométrique
Une suite $(u_n)$ est géométrique s'il existe un réel $q$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n\times q$
$q$ est la raison de la suite.
Le quotient de deux termes consécutifs est égal à la raison soit $\dfrac{u_{n+1}}{u_n}=q$Aide
On a $v_{n+1}=u_{n+1}-20=1,1u_{n} -2-20$
Il faut montrer que pour tout entier $n$, il existe un réel $q$ tel que $v_{n+1}=qv_n$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer $v_{n}$ en fonction de $n$.
Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$Aide
On a $(v_n)$ une suite géométrique de raison $q=1,1$ et de premier terme $v_1=10$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire que pour tout entier naturel $n$: $ u_{n} = 20+10\times 1,1^{n-1}$.
Aide
0 On a $v_n=u_n-20$ donc $u_n=v_n+20$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie B
Une chaîne de télévision compte 30 000 abonnés au mois de janvier (mois \no 1).
Elle fait une campagne de publicité pour augmenter le nombre d'abonnés.
Ce qui lui permet chaque mois d'avoir 10% d'abonnés supplémentaires mais perd 2000 anciens abonnés.
- Montrer que cette situation peut être modélisée par la suite $\left(u_{n}\right)$ où $u_{n}$ désigne le nombre de milliers d'abonnés le n$^{\text{ième}}$ mois de la campagne publicitaire.
Aide
1 Augmenter une valeur de 10% revient à appliquer le coefficient multiplicateur $1+\dfrac{10}{100}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On décide d'utiliser un algorithme pour afficher le nombre d'abonnés le n$^{\text{ième}}$ mois de la campagne publicitaire.
Compléter l'algorithme ci-dessous pour qu'il affiche le nombre d'abonnés le n$^{\text{ième}}$ mois.

Aide
2 On peut utiliser la suite donnée sous forme récurrente donnée dans l'énoncé.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer le nombre d'abonnés au mois de décembre.
Aide
3 Le mois de janvier est le premier mois soit $n=1$ et donc pour le mois de décembre, on a $n=12$
Le nombre d'abonnés est en milliers donc il faut arrondir aux millièmes.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message