Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Produit de facteurs nul
Racines d’un polynôme de degré 3
Ressources associées et exercices semblables
Recherche de tangentes parallèles (réf 0561)
exercice
Position relative d’une courbe et d’une tangente (réf 0569)
exercice
Vidéo de l’exercice
Ci-dessous, on donne le tracé de $C_f$ sur l'intervalle $[-1;3]$.
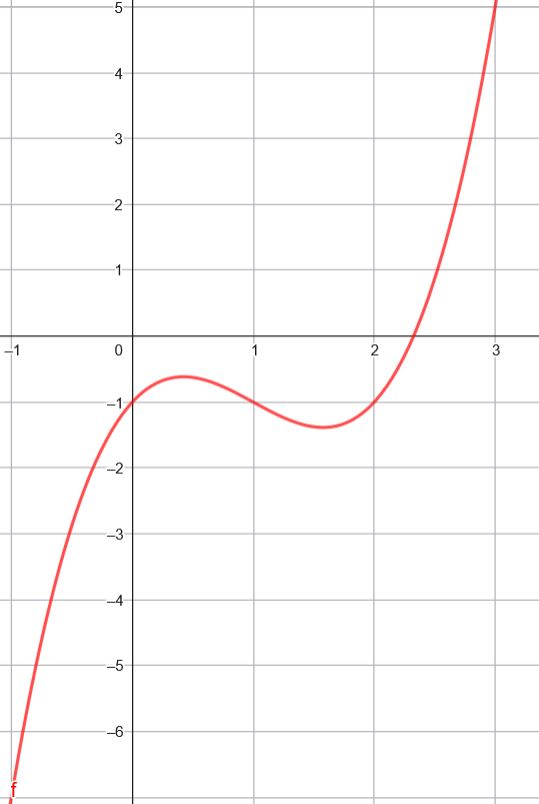
On veut déterminer les abscisses des points de la courbe pour lesquels la tangente passe par l'origine du repère.
- Conjecturer les abscisses de ces points en utilisant le graphique.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Démontrer la conjecture émise à la question 1 en donnant les valeurs exactes des abscisses des deux points.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Aide
Si on note $\alpha$ l'abscisse d'un tel point, il faut exprimer l'équation réduite de la tangente en fonction de $\alpha$ et ensuite le point $O(0;0)$ doit vérifier cette équation de droite
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements