Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Sens de variation d’une fonction affine
Représenter une fonction affine (droite)
Antécédent de 0 par une fonction affine
Ressources associées et exercices semblables
signe de f(x)=ax+b (réf 0142)
exercice
- $f(x)=2x-3$
Rappel cours
Fonction affine
Une fonction afffine est définie sur $\mathbb{R}$ par $f(x)=ax+b$.
La représentation graphique d'une fonction affine est une droite coupant l'axe des ordonnées au point $(0;b)$ et l'axe des abscisses au point $\left(\dfrac{-b}{a}\right)$ (si $a\neq 0$).
Si $a=0$ alors la droite est parallèle à l'axe des abscisses.Aide
Il faut déterminer le signe du coefficient de $x$ pour déterminer le sens de variation
On peut calculer deux images pour représenter $f$, par exemple $f(0)$ et $f(2)$
Il faut résoudre l'équation $f(x)=0$ ensuiteSolution
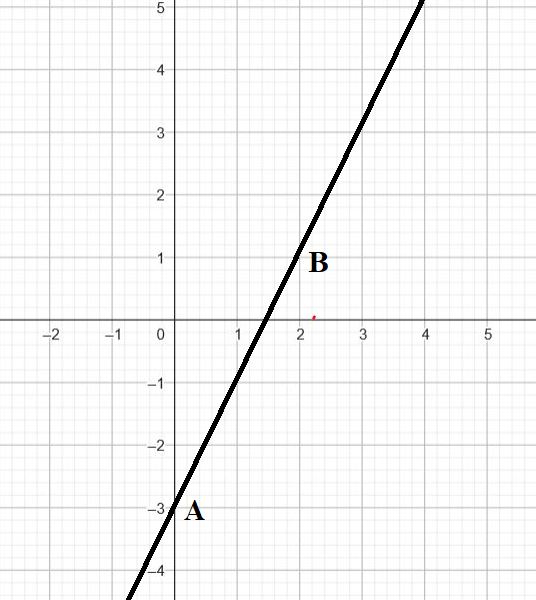
$f(x)=2x-3=ax+b$ avec $a=2$ et $b=-3$
$f(0)=-3$
$f(2)=2\times 2-3=1$
On place donc les points $A(0;-3)$ et $B(2;1)$
$f(x)=0\Longleftrightarrow 2x-3=0$
$\phantom{f(x)=0}\Longleftrightarrow 2x=3$
$\phantom{f(x)=0}\Longleftrightarrow x=\dfrac{3}{2}$
- $f(x)=-2x+4$
Aide
Il faut déterminer le signe du coefficient de $x$ pour déterminer le sens de variation
On peut calculer deux images pour représenter $f$, par exemple $f(0)$ et $f(3)$
Il faut résoudre l'équation $f(x)=0$ ensuiteSolution
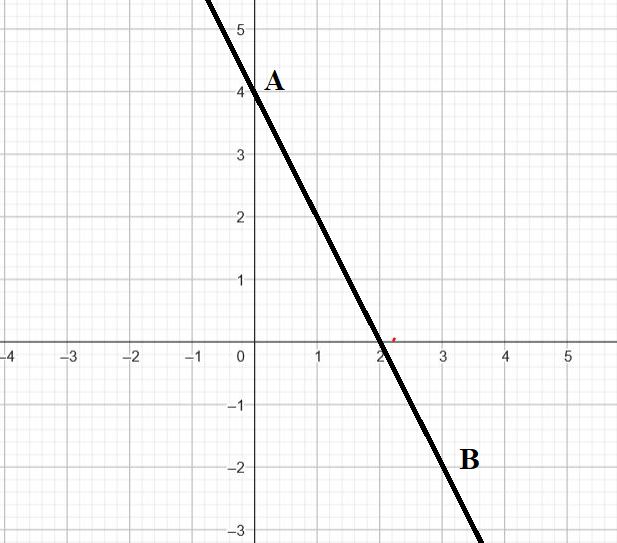
$f(x)=-2x+4=ax+b$ avec $a=-2$ et $b=4$
$f(0)=4$
$f(3)=-2\times 3+4=-2$
On place donc les points $A(0;4)$ et $B(3;-2)$
$f(x)=0\Longleftrightarrow -2x+4=0$
$\phantom{f(x)=0}\Longleftrightarrow -2x=-4$
$\phantom{f(x)=0}\Longleftrightarrow x=\dfrac{-4}{-2}=2$
- $f(x)=3-x$
Solution
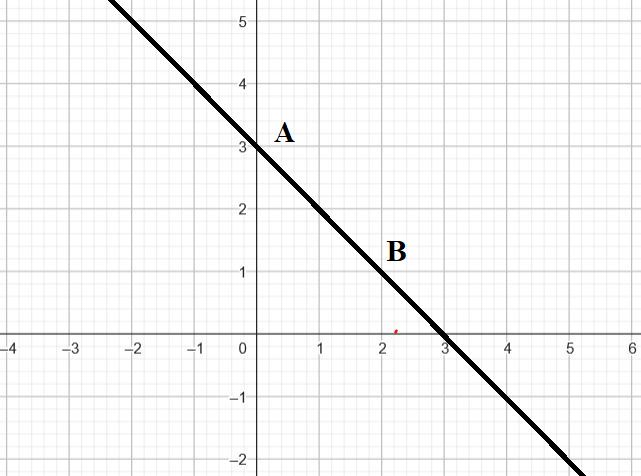
$f(x)=3-x=-x+3=ax+b$ avec $a=-1$ et $b=3$
$f(0)=3$
$f(2)=3-2=1$
On place donc les points $A(0;3)$ et $B(2;1)$
$f(x)=0\Longleftrightarrow 3-x=0$
$\phantom{f(x)=0}\Longleftrightarrow -x=-3$
$\phantom{f(x)=0}\Longleftrightarrow x=3$


 Envoyez votre message
Envoyez votre message