Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lecture graphique d’images et d’antécédents
Calculs d’images et d’antécédents
Ressources associées et exercices semblables
devoir fonctions (réf 0231)
devoir
fiche méthode images et antécédents (réf 233)
fiche méthode tableau de variation d’une fonction (réf 0234)
méthode
- $f(x)=\dfrac{3}{3x-2}$
Rappel cours
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Aide
Il faut que le dénominateur soit différent de zéro.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $g(x)=\sqrt{6-2x}$
Aide
On ne peut calculer une racine carrée qu'avec des nombres supérieurs ou égaux à 0
Il faut que $6-2x$ soit supérieur ou égal à 0.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $h(x)=\dfrac{2}{x}+\sqrt{x}$
Aide
Il y a deux conditions à respecter pour chacun des deux termes de la somme.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Quelle est l'image de 3 par $f$ ?
Rappel cours
Calcul d'une image
Pour calculer l'image d'un nombre $\alpha$ appartenant à l'ensemble de définition de $f$ il faut remplacer $x$ par la valeur $\alpha$ dans l'expression de $f$.
Par exemple si $f$ est définie sur $\mathbb{R}$ par $f(x)=-2x^2+5x-1$ alors l'image de $-2$ par $f$ est:
$f(-2)=-2\times (-2)^2+5\times (-2)-1$
$\phantom{f(-2)}=-8-10-1$
$\phantom{f(-2)}=-2\times 4-10-1$
$\phantom{f(-2)}=-19$
Remarque: On peut calculer des images en utilisant le MENU TABLE de la calculatrice.
Aide
Il faut remplacer $x$ par 3 dans l'expression de $f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quelle est l'image de $-2$ par $f$ ?
Aide
Il faut remplacer $x$ par $-2$ dans l'expression de $f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer le ou les antécédents de 5 par $f$.
Rappel cours
Calcul d'un (des) antécédent(s)
Pour rechercher les antécédents d'un nombre $\alpha$ par une fonction $f$ définie sur $D_f$, il faut résoudre l'équation $f(x)=\alpha$.
Les valeurs trouvées doivent appartenir à $D_f$.Aide
Il faut déterminer les valeurs de $x$ pour lesquelles $f(x)=5$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer le ou les antécédents de $-3$ par $f$.
Aide
Il faut déterminer les valeurs de $x$ pour lesquelles $f(x)=-3$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
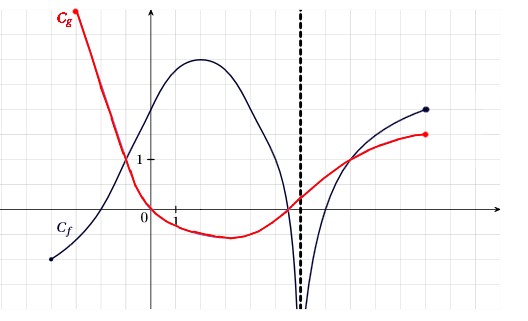
Répondre aux questions suivantes avec la précision permise par la figure.
- Déterminer les ensembles de définition $D_f$ et $D_g$ de $f$ et $g$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer l'image de 2 par $f$ puis par $g$.
Aide
Il faut déterminer l'ordonnée du point de la courbe d'abscisse 2 dans chacun des cas.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les antécédents de $1$ par $f$ (justifier la réponse par une phrase).
Aide
Il faut déterminer les abscisses des points de la courbe dont l'ordonnée est 1.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre graphiquement l'inéquation $f(x)\geq 2$.
Aide
Il faut déterminer les abscisses des points de la courbe dont l'ordonnée est supérieure ou égale à 2.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre graphiquement l'inéquation $f(x)= g(x)$.
Aide
On cherche les abscisses des points de la courbe $C_f$ ayant la même ordonnée que les points de la courbe $C_g$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre graphiquement l'inéquation $f(x) > g(x)$.
Aide
Il faut déterminer les abscisses des points de la courbe $C_f$ dont l'ordonnée est strictement supérieure aux ordonnées des points de $C_g$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de signe de $g(x)$.
Aide
$g(x)>0$ quand la courbe est au-dessus de l'axe des abscisses
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
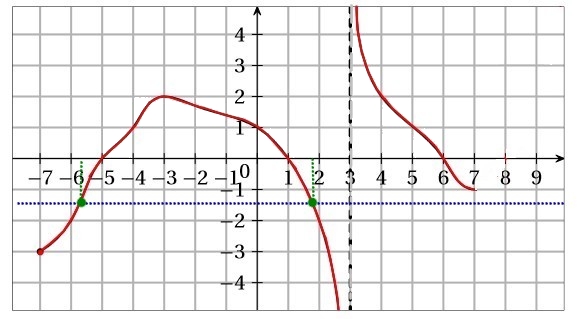
- Dresser le tableau de variation de $f$.
Rappel cours
Tableau de variation
$f$ est une fonction définie sur un intervalle I de $\mathbb{R}$ et $C_f$ sa représentation graphique.
Le tableau de variation de $f$ permet de visualiser les variations de $f$ ainsi que ses extremums (maximum ou minimum).
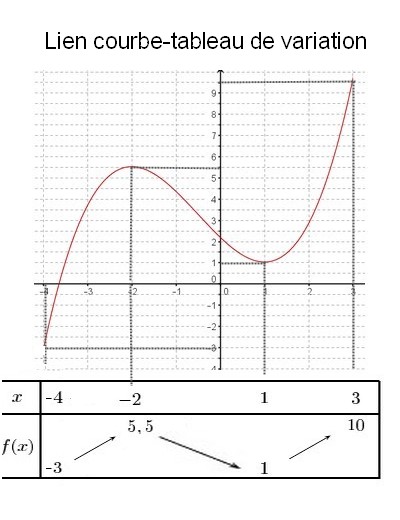
Aide
Il faut placer les valeurs données dans l'ensemble de définition $x=-7$, $x=3$ et $x=9$ puis les valeurs de $x$ pour lesquelles le sens de variation change.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer en fonction des valeurs prises par le réel $k$, le nombre de solutions de l'équation $f(x)=k$.
Aide
Il faut distinguer plusieurs cas possibles pour déterminer le nombre de points d'intersection de la courbe et de la droite d'équation $y=k$ (droite parallèle à l'axe des abscisses passant par l'ordonnée $k$).
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message