Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Fonctions et tableau de variations
Dresser le tableau de variation d’une fonction
Lecture d’un tableau de variation
Ressources associées et exercices semblables
fiche méthode tableau de variation d’une fonction (réf 0234)
méthode
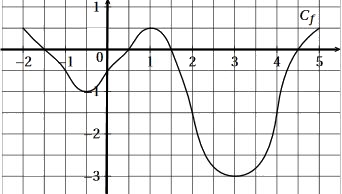
- Quel est l'ensemble de définition de $f$?
Rappel cours
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Aide
Il faut déterminer les valeurs de $x$ pour lesquelles l'image par $f$ existe
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de variation de $f$.
Rappel cours
Tableau de variation
$f$ est une fonction définie sur un intervalle I de $\mathbb{R}$ et $C_f$ sa représentation graphique.
Le tableau de variation de $f$ permet de visualiser les variations de $f$ ainsi que ses extremums (maximum ou minimum).
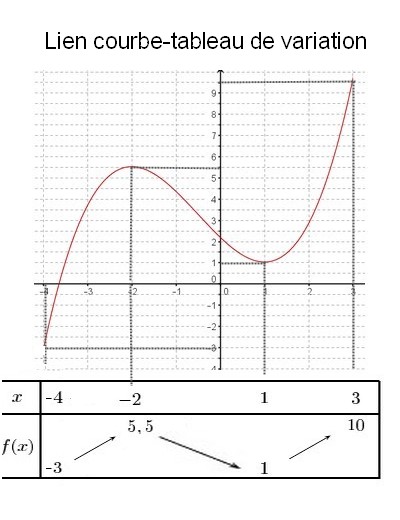
Aide
Les valeurs de $x$ pour lesquelles le sens de variation change sont $-1$, $1$ et $3$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Comparer $f(2)$ et $f(2,5)$.
Aide
Il faut utiliser le sens de variation de $f$ sur $[1;3]$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Dresser le tableau de signe de $f(x)$.
Aide
$f(x)>0$ quand la courbe est au-dessus de l'axe des abscisses
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quel est le minimum de $f$?
Rappel cours
Extremums d'une fonction: maximum et minimum
$f$ est une fonction définie sur un intervalle I de $\mathbb{R}$.
Le maximum de $f$ sur I, s'il existe est le réel $M$ tel que pour tout réel $x$ de I, on a $f(x)\leq M$
Le minimum de $f$ sur I, s'il existe est le réel $m$ tel que pour tout réel $x$ de I, on a $f(x)\geq m$
$f$ admet un extremum sur I si $f$ admet un maximum ou un minimum sur I.
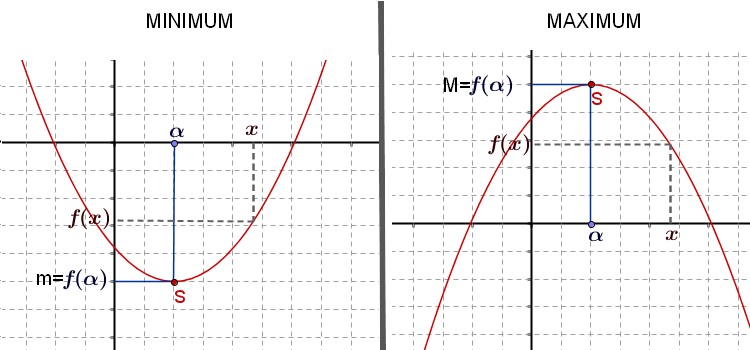
Le maximum ou le minimum se lit sur l'axe des ordonnées sur le graphique.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
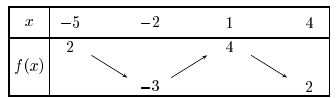
- Quel est l'ensemble de définition de $f$?
Aide
Il faut lire la première ligne du tableau
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quels sont les extremums de $f$?
Rappel cours
Extremums d'une fonction: maximum et minimum
$f$ est une fonction définie sur un intervalle I de $\mathbb{R}$.
Le maximum de $f$ sur I, s'il existe est le réel $M$ tel que pour tout réel $x$ de I, on a $f(x)\leq M$
Le minimum de $f$ sur I, s'il existe est le réel $m$ tel que pour tout réel $x$ de I, on a $f(x)\geq m$
$f$ admet un extremum sur I si $f$ admet un maximum ou un minimum sur I.

Le maximum ou le minimum se lit sur l'axe des ordonnées sur le graphique.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On donne de plus les informations suivantes:
- L'image de 3 par $f$ est 3
- les antécédents de 0 par $f$ sont $-3$ et $-1$.
Tracer une représentation graphique possible de $f$ en respectant ces informations.Rappel cours
Représentation graphique
Soit $f$ une fonction définie sur un sous-ensemble $\mathcal{D}$ de $\mathbb{R}$.
La courbe représentative de $f$ est l'ensemble des points du plan (muni d'un repère) de coordonnées $(x;f(x))$ avec $x\in \mathcal{D}$.
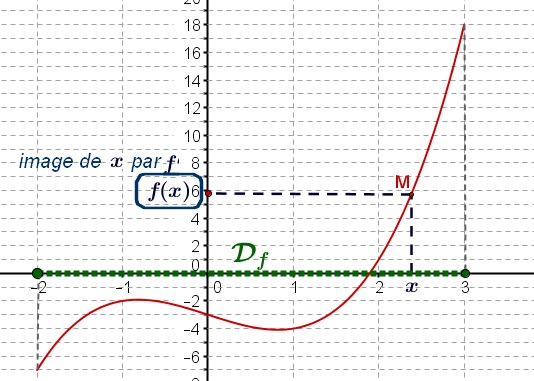
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message