Équations cartésiennes (réf 0399) chapitre 7: équations de droites, MATHÉMATIQUES SECONDE, séquence 5 exercices de synthèse et devoirs d'entraînement

Home MATHÉMATIQUES SECONDE chapitre 7: équations de droites séquence 5 exercices de synthèse et devoirs d'entraînement

Équations cartésiennes (réf 0399)

Ressource précédente: Devoir complet fin de chapitre (réf 0397) Ressource suivante: Fiche méthode équation réduite d’une droite (réf 0400)

Informations

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Déterminer une équation cartésienne
Intersection de deux droites
Milieu d’un segment et équation d’une médiane
Centre de gravité

Ressources associées et exercices semblables

Devoir corrigé sur les équations cartésiennes(réf 0396)
devoir

Fiche méthode équation réduite d’une droite (réf 0400)
méthode

| | | |

Exercice 1 (12 points)

Le plan est muni d'un repère orthonormé.
On donne les points $A(3;1)$, $B(5;4)$ et $C(-1;-1)$.

Déterminer une équation cartésienne de la droite $(AB)$ et tracer $(AB)$ dans le repère ci-dessous.

Aide

$\overrightarrow{AB}$ est un vecteur directeur de la droite $(AB)$
$M(x;y)\in (AB)$ si et seulement si $\overrightarrow{AM}$ et $\overrightarrow{AB}$ sont colinéaires

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer les coordonnées des points d'intersections $A'$ et $B'$ de la droite $(AB)$ avec les axes du repère.

Aide

On a donc $y_{A'}=0$ et $x_B'}=0$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer une équation cartésienne de la droite $(d)$ passant par $C$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix} -2\\1\end{pmatrix}$ puis la tracer dans le repère ci-dessous.

Aide

$\overrightarrow{u}$ est un vecteur directeur de $(d)$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer les coordonnées du point d'intersection $I$ des droites $(AB)$ et $(d)$.

Aide

Il faut résoudre le système formé avec les équations des droites $(AB)$ et $(d)$.
On peut utiliser la méthode des combinaisons en multipliant chaque membre de l'équation de $(AB)$ par 3 et chaque membre de l'équation de $(d)$ par 2

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer une équation cartésienne de la droite $(d')$ parallèle à $(AC)$ passant par $D(5;0)$.

Aide

$\overrightarrow{AC}$ est un vecteur directeur de $(d')$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Montrer que les droites $(d)$, $(AB)$ et $(d')$ sont concourantes en I.

Aide

Il faut vérifier le point $I$ appartient à $(AB)$, $(d)$ et $(d')$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Exercice 2 (8 points)

$ABC$ est un triangle avec $A(-2;1)$, $B(4;5)$ et $C(4;-3)$.
On note $D$ le milieu de $BC]$ et $E$ le milieu de $[AC]$
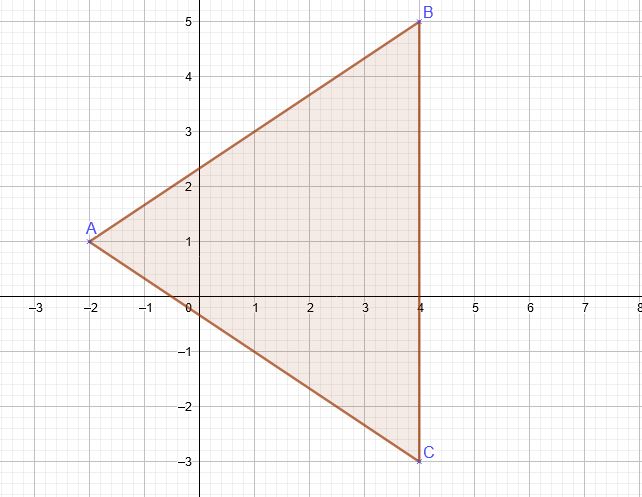
droites dans un repère

Tracer $(AD)$ et $(BE)$.
Que représentent ces deux droites pour le triangle?

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Sans calculs, donner une équation de $(AD)$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Graphiquement, déterminer l'équation réduite de $(BE)$

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Déterminer par le calcul les coordonnées du point d'intersection $G$ des droites $(AD)$ et $(BE)$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On note $H$ le milieu de $[AB]$.
Déterminer par le calcul une équation cartésienne de $(CH)$.
Le point $G$ appartient-il à $(CH)$?

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Que représente $G$ pour le triangle $ABC$?
Sans calculs, justifier que $G$ appartient à la droite $(CF)$ avec $F$ milieu de $[AB]$.

Solution

Vous devez être abonné pour accéder à ce contenu...
Infos abonnements

Vous devez être abonné pour accéder à ce contenu...

Infos abonnements

Ressource précédente: Devoir complet fin de chapitre (réf 0397) Ressource suivante: Fiche méthode équation réduite d’une droite (réf 0400)