Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Recettes
Bénéfices
Résolution d’une inéquation avec un produit de facteurs
Ressources associées et exercices semblables
L'entreprise a une capacité de production mensuelle maximale de 300 climatiseurs.
Chaque climatiseur est vendu 8900 euros et on suppose que toute la production est vendue.
- Exprimer en fonction de $q$ le coût de production $C_m(q)$ d'un climatiseur (coût moyen de production) quand on en produit une quantité $q$ dans le mois.
Aide
Le coût moyen par climatiseur est le coût total divisé par le nombre total de climatiseurs produits.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Vérifier que $C_m(q)=(q-150)^2+2500$.
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
On peut développer l'expression proposée
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $C_m(150)$.
et en déduire que le minimum de la fonction $C_m$ est 2500 pour une production mensuelle de 150 climatiseurs.
Quel est alors le bénéfice mensuel de l'entreprise?Rappel cours
Comparer deux nombres
Soit $a$ et $b$ deux nombres réels, $a < b$ si et seulement si $b-a>0$
Conséquence: Pour comparer deux nombres ou deux expressions, on peut étudier le signe de leur différence.Aide
On veut comparer $C_m(q)$ et $2500$ en utilisant l'expression de la question précédente.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer, en fonction de $q$, la recette totale mensuelle de l'entreprise.
Aide
La recette correspond à la somme récoltée pour $q$ climatiseurs vendus.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer le bénéfice total mensuel $B(q)$ de l'entreprise en fonction de $q$.
Aide
Le bénéfice est égal à la recette diminuée des coût de production
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer le bénéfice de l'entreprise $B_m(q)$ sur chaque climatiseur(bénéfice moyen) en fonction de $q$ quand la production mensuelle est de $q$ climatiseurs.
Aide
Le bénéfice moyen correspond au bénéfice total divisé par le nombre total de climatiseurs vendus.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que pour tout réel $q\in[0;300]$, $B_m(q)=6400-(q-150)^2$ puis factoriser $B_m(q)$
Aide
On peut développer l'expression proposée
signe $-$ devant la parenthèseSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Résoudre $B_m(q)\geq 0$ et en déduire le nombre d'objets à fabriquer pour que l'entreprise ne soit pas en déficit.
Rappel cours
Identités remarquables
$(a+b)^2=a^2+2ab+b^2$
$(a-b)^2=a^2-2ab+b^2$
$(a-b)(a+b)=a^2-b^2$
Aide
Il faut factoriser $B_m(q)$ en utilisant la question précédente
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On donne ci-dessous les représentations graphiques $C_C$ et $C_R$ respectivement des fonctions coût ($C$) et recette ($R$).
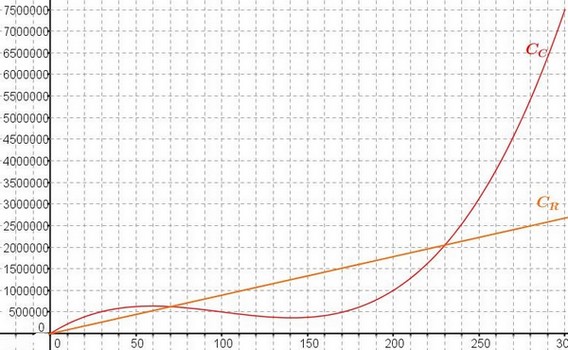
Comment peut-on contrôler le résultat de la question précédente?Aide
L'entreprise n'est pas en déficit si la recette est supérieure au coût de production.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message