Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Vocabulaire des matrices
Inverse d’une matrice carrée d’ordre 2
Produit de deux matrices
Ressources associées et exercices semblables
Devoir matrices, calculs avec les matrices, systèmes d’équations (réf 1642)
devoir
Devoir complet matrices, opérations sur les matrices et systèmes d’équations (réf 1641)
devoir
- Donner une matrice ligne à coefficients entiers distincts compris entre $0$ et $6$.
Rappel cours
Matrice ligne et colonne
Une matrice de dimensions $1\times p$ ( à une ligne) est appelée matrice ligne.
Une matrice de dimensions $n\times 1$ ( à une colonne) est appelée matrice colonneSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Écrire la matrice carrée d'ordre 4 telle que :
$a_{ij}=
\begin{cases}
0 & si~~i=j \\
1 & si~~i>j\\
i+j & si~~i
Rappel cours
Matrice nxp
Une matrice de dimansions $n\times p$ est un tableau de nombres réels à $n$ lignes et $p$ colonnes.
On a $M=\begin{pmatrix}a_{11}&a_{12}&a_{13}&....&a_{1p}\\ a_{21}&a_{22}&a_{23}&....&a_{2p}\\ .&.&.&...&.\\ .&.&.&...&.\\ .&.&.&...&.\\ .&.&.&...&.\\ .&.&.&...&.\\ a_{n1}&a_{n2}&a_{n3}&....&a_{np} \end{pmatrix}$
On note $M=(a_{ij})$ où $a_{ij}$ est le coefficient de la $i$ ième ligne et de la $j$ ième colonne.Aide
Si $i=j$ alors c'est un coefficient de la diagonale
Si $i < j$ alors c'est un coefficient qui est au-dessus de la diagonaleSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Calculer $C=A\times B$. Détailler les calculs.
Rappel cours
Produit de deux matrices
Le produit de la matrice $A=(a_{ij})$ de dimensions $n\times p$ par la matrice $B=(b_{ij})$ de dimensions $p\times m$ est la matrice $C=(c_{ij})=A\times B$ de dimensions $n\times m$ telle que $c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}=\sum_k=1^p a_{ik}b_{kj}$}
Schématiquement on a:
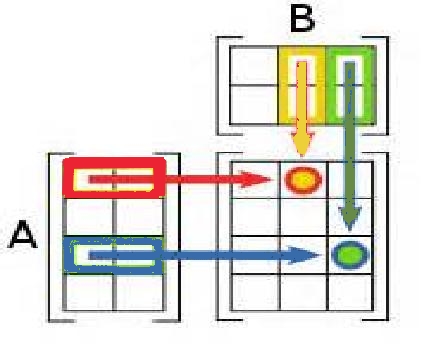
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements- Peut-on calculer $B\times A$ ? Expliquer.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnementsExercice 3 (2,5 points)Déterminer, si c'est possible, l'inverse de chacune des matrices $A$ et $B$ ci-dessous : $A=\begin{pmatrix}2&3\\1&-1\end{pmatrix}$ et$B=\begin{pmatrix}3&6\\4&8\end{pmatrix}$Rappel cours
Déterminant d'une matrice carrée d'ordre 2
Soit $A=\begin{pmatrix} a&b\\c&d \end{pmatrix}$
le déterminant de $A$ noté $det(A)$ est le réel $det(A)=ad-bc$}
Inverse d'une matrice carrée d'ordre 2
Soit $A=\begin{pmatrix} a&b\\c&d \end{pmatrix}$ telle que $det(A)\neq 0$.
$A^{-1}=\dfrac{1}{det(A)}\begin{pmatrix} d&-b\\-c&a \end{pmatrix}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnementsExercice 4 (3 points)On considère la matrice $A=\begin{pmatrix} 0&1&-1\\-1&2&-1\\1&-1&2 \end{pmatrix}$- Démontrer que $A^2=3A-2I_{3}$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Peut-on calculer $B\times A$ ? Expliquer.
- En déduire que $A$ est inversible et donner l'expression de $A^{-1}$ en fonction de $A$.
Rappel cours
Inverse d'une matrice carrée d'ordre $n$
Soit $A$ une matrice carrée d'ordre $n$, $A$ est un inversible s'il existe une matrice carrée d'ordre $n$ notée $A^{-1}$ telle que $A\times A^{-1}=I_n$Aide
$A^2-3AA(A-3I_3)=2I_3$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Expliciter $A^{-1}$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Infos abonnements


 Envoyez votre message
Envoyez votre message