Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Calculs avec les matrices
Suites et matrices: raisonnement par récurrence
Ressources associées et exercices semblables
Suites et matrices (réf 1638)
exercice
et $\begin{cases} b_0=2\\ b_{n+1}=a_n+5b_n~~pour~~n\in\mathbb{N} \end{cases}$
On note $(U_n)$ la suite de matrices définies par $U_n=\begin{pmatrix} a_n\\b_n\end{pmatrix}$ pour $n\in \mathbb {N}$.
- Déterminer une $A$ telle que $U_{n+1}=AU_n$.
Rappel cours
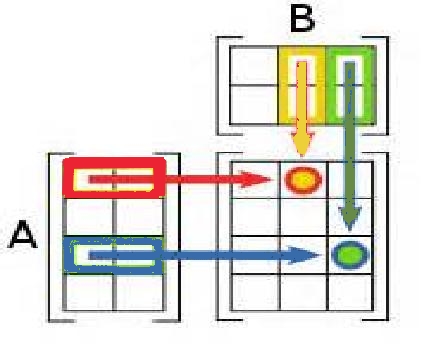
Produit de deux matrices
Le produit de la matrice $A=(a_{ij})$ de dimensions $n\times p$ par la matrice $B=(b_{ij})$ de dimensions $p\times m$ est la matrice $C=(c_{ij})=A\times B$ de dimensions $n\times m$ telle que $c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+...+a_{ip}b_{pj}=\sum_k=1^p a_{ik}b_{kj}$}
Schématiquement on a:
Aide
La matrice $A$ est donc une matrice carrée $2\times 2$
Ecrire une égalité de deux matrices et identifier les coefficientsSolution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Donner $U_0$ et montrer par récurrence alors que $U_n=A^nU_0$
Rappel cours
Raisonnement par récurrence
On considère une propriété notée $P_n$ avec $n \in \mathbb{N}$.
- $P_0$ vraie
- Si $P_n$ est vraie alors $P_{n+1}$ est vraie.
On a alors $P_n$ vraie pour tout entier naturel $n$.Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message