Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Position relative de deux courbes
Aire sous la courbe et calcul d’intégrales
Calcul de l’aire entre deux courbes
Ressources associées et exercices semblables
Aire entre deux courbes (réf 1219)
exercice
On donne ci-dessous les représentations graphiques $(C_f)$ et $C_g$ respectivement des fonctions $f$ et $g$.
- En utilisant le quadrillage, donner un encadrement, en unités d'aires, de l'aire $\mathcal{A}$ du domaine limité par $C_f$, $C_g$ et les droites d'équations $x=-1$ et $x=1$.
Aide
Une unité d'aire contient 4 carreaux du quadrillage.
Il faut déterminer le nombre de carreaux du quadrillage contenus dans le domaine cité et le nombre de carreaux entiers contenant le domaine cité ci-dessus.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer graphiquement le signe de $f(x)-g(x)$ sur $[-1;1]$.
Aide
Il faut étudier la position relative de $C_f$ et $C_g$ sur $[-1;1]$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer la valeur exacte de cette aire.
Rappel cours
Primitives des fonctions usuelles
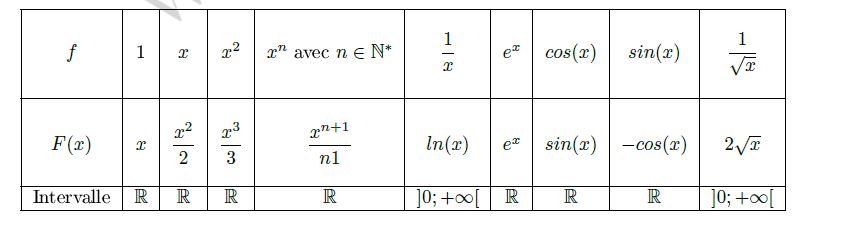Intégrale
La fonction $f$ est continue sur $[ab]$ et $F$ est une primitive de $f$ sur $[a;b]$
$\int_a^b f(x)dx=[F(x)]_a^b=F(b)-F(a)$Aide
Il faut utiliser le fait que $f(x)>g(x)>0$ sur $[-1;1]$ et $f$ et $g$ sont continues sur $\mathbb{R}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements