Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Limites d’une fonction rationnelle
Asymptote oblique et position relative de la courbe et de l’asymptote
Ressources associées et exercices semblables
Asymptote oblique (réf 1013)
exercice
- Déterminer les limites de $f$ en $0$ et préciser la ou les asymptotes éventuelles à la courbe.
Rappel cours
Opérations sur les limites
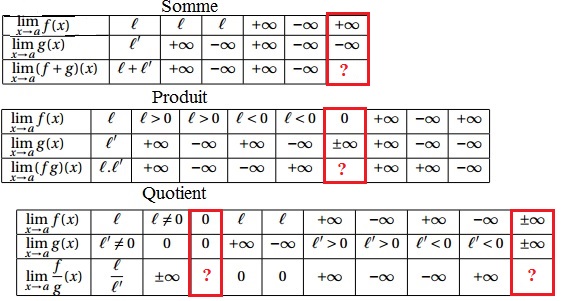
Aide
Il faut distinguer les cas $x<0$ et $x>0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les limites de $f$ en $-\infty$ et $+\infty$
Aide
On peut chercher à factoriser $x^2$ au numérateur
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On considère la droite $\Delta$ d'équation réduite $y=\dfrac{x}{2}-1$
Montrer que $f(x)-\left(\dfrac{x}{2}-1\right)=\dfrac{x^2-2x+4}{2x}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les limites en $-\infty$ et $+\infty$ de $f(x)-\left(\dfrac{x}{2}-1\right)$.
Que représente alors la droite $\Delta$ pour la courbe $C_f$?Aide
La limite en $+\inty$ ou $-\infty$ de $f(x)-\left(\dfrac{x}{2}-1\right)$ représnte "l'écart" entre la droite et la courbe quand $x\longrightarrow \pm \infty$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la position relative de $\Delta$ par rapport à $C_f$.
Aide
Il faut déterminer le signe de $f(x)-\left(\dfrac{x}{2}-1\right)$ pour savoir si $\Delta$ est au-dessus ou en-dessous de $C_f$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Tracer $C_f$, $\Delta$ et l'asymptote verticale dans un repère orthonormé.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message