Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lecture graphique du nombre dérivé
Étude des variations et limites d’une fonction avec ln
Dérivée seconde et convexité
Ressources associées et exercices semblables
Devoir complet fin de chapitre trois ex BAC 2023 (réf 1131)
devoir
Devoir fin de chapitre équations, inéquations et étude de fonction avec ln (réf 1132)
devoir
Vidéo de l’exercice
On donne ci-dessous $C_f$ la représentation graphique de $f$ dans un repère orthogonal et T la tangente à la courbe au point $A$ d'abscisse 1.
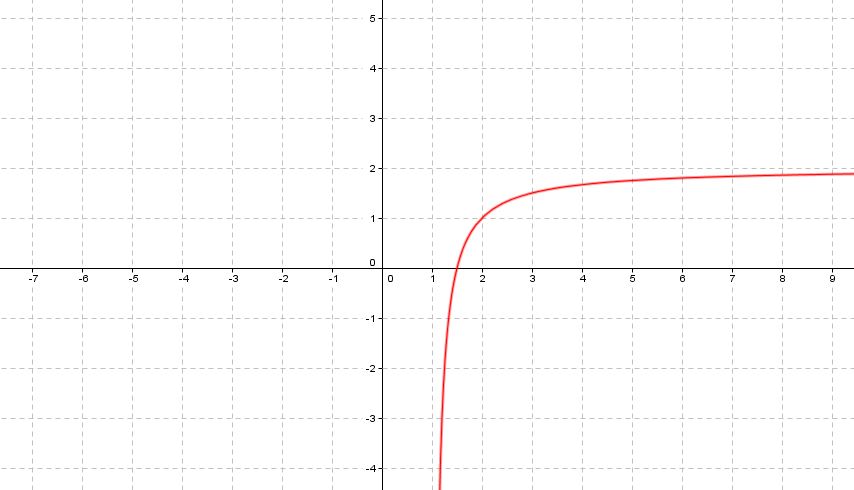
- Déterminer graphiquement $f(1)$ et $f~'(1)$
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Aide
Il faut déterminer le coefficient directeur de T.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Exprimer $f~'(x)$ en fonction de $a$ et $b$.
Rappel cours
Dérivée de la fonction ln
La fonction $ln$ est dérivable sur $]0;+\infty[$ et $(ln(x))'=\dfrac{1}{x}$Aide
On a $f(x)=ax+b\times ln(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant la question 1, déterminer les réels $a$ et $b$.
Aide
On a $f(1)=2$ et il faut exprimer $f(x)$ en fonction de $a$ et $b$.
De même on a $f~'(1)=-2$ et il faut exprimer $f~'(1)$ en fonction de $a$ et $b$.
Rappel: $ln(1)=0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les limites de $f$ en $0$ et $+\infty$
Rappel cours
Limites de ln
$\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$
$\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$ Croissances comparées
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{ln(x)}{x}=0$
$\displaystyle \lim_{x \rightarrow 0^+}xln(x)=0$Aide
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer alors les variations de $f$ et dresser sont tableau de variations.
Aide
On a obtenu à la question 2., $f~'(x)=a+\dfrac{b}{x}$ avec $a=2$ et $b=-4$
Il faut étudier le signe de $f~'(x)$ en réduisant au préalable au même dénominateur
Rappel: $x\in ]0;+\infty[$ donc $x>0$ ....Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $f~''(x)$ et en déduire la convexité de $f$.
Rappel cours
point d'inflexion et dérivée seconde
si $f"(x)$ s'annule et change de signe en $x=x_A$ alors la courbe admet un point d'inflexion au point $A$.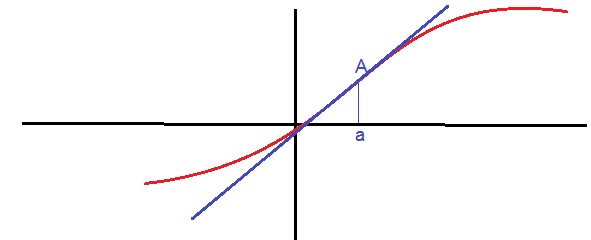
Aide
On a $f~'(x)=\dfrac{2x-4}{x}$
On pose $u(x)=2x-4$ et $v(x)=x$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message