Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Position relative de droites et de plans
Construction d’intersections dans l’espace
Ressources associées et exercices semblables
Constructions d’intersections dans l’espace (réf 1300)
exercice
Position de droites et de plans-intersections dans l’espace (réf 1302)
exercice
Fiche méthode représentation paramétrique d’une droite (réf 1295)
méthode
Vidéo de l’exercice
- Justifier que les droites $(IJ)$ et $(AH)$ sont sécantes en $M$ puis construire le point $M$.
Rappel cours
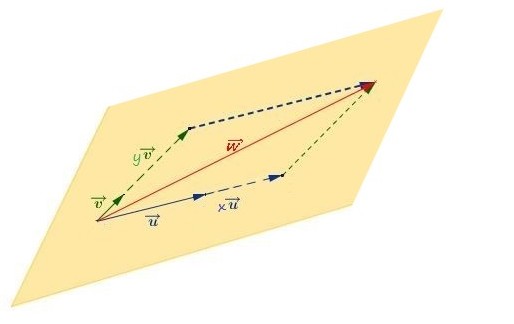
vecteurs coplanaires
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
Aide
Il faut justifier que les deux droites sont contenues dans un même plan.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Construire le point d'intersection $N$ de la droites $(IJ)$ et du plan $(BEF)$.
Aide
Il faut utiliser deux droites coplanaires (contenues dans un même plan).
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - $K$ est un point du segment $[DC]$ tel que $DK\neq AI$.
Tracer l'intersection du plan $(IJK)$ et du plan $(DCF)$.Rappel cours
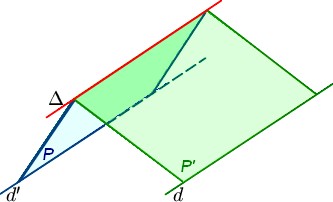
théorème du toit
Lorsque deux plans $P$ et $P'$ sont sécants et contiennent respectivement les droites $d$ et $d'$, l'intersection de $P$ et de $P'$ est une droite $\Delta$ parallèle à $d$ et à $d'$.
Aide
Il faut utiliser le fait que les plans $(ABE)$ et $(DCF)$ sont parallèles (faces opposées du pavé droit).
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire l'intersection des plans $(IJK)$ et $(BEF)$.
Aide
Le point $N$ appartient aux plans $(IJK)$ et $(BEF)$
Il faut trouver un second point d'intersection des deux plans en utilisant la droite de la quation précédente et la droite $(CF)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements