Convexité avec un polynôme de degré 3 (réf 1069) Chapitre 3 dérivation, continuité et convexité, séquence 5 exercices de synthèse et devoirs d'entraînement, TERMINALE SPÉCIALITÉ MATHS - MATHS-LYCEE

contact@maths-lycee.fr

(+33) 07 59 58 68 37

Home TERMINALE SPÉCIALITÉ MATHS Chapitre 3 dérivation, continuité et convexité séquence 5 exercices de synthèse et devoirs d'entraînement

Convexité avec un polynôme de degré 3 (réf 1069)

Ressource précédente: Étude de la convexité d’une fonction avec une exponentielle (réf 1066) Ressource suivante: Étude d’une fonction avec exponentielle (extrait BAC) (réf 1070)

Infos

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Dérivée seconde

Signe de la dérivée seconde et convexité

Équation réduite d’une tangente

Ressources associées et exercices semblables

Devoir convexité (réf 1075)
devoir

| | | |

$f$ est une fonction définie et deux fois dérivable sur $\mathbb{R}$ définie par $f(x)=ax^3+6x^2-3x+1$ avec $a$ réel.

Calculer la dérivée seconde $f~''$ de $f$

Aide

$a$ est le coefficient de $x^3$

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
En déduire la valeur de $a$ pour que fonction $f$ soit concave sur $[1;+\infty[$ et convexe $]-\infty;1]$

Rappel cours

point d'inflexion et dérivée seconde
si $f"(x)$ s'annule et change de signe en $x=x_A$ alors la courbe admet un point d'inflexion au point $A$.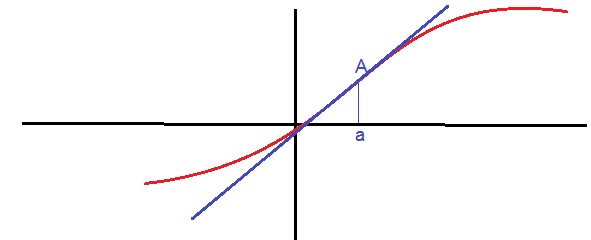

Aide

Il faut résoudre l'équation $f~''(1)=0$

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Déterminer l'équation de la tangente $T$ à la courbe au point d'abscisse $x=1$

Rappel cours

Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$

Aide

Calculer $f(1)$ puis $f'(1)$

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Tracer la courbe représentative de $f$ et la tangente $T$ dans un repère orthogonal et contrôler les résultats obtenus

Aide

Avec GEOGEBRA, on peut saisir la fonction $f$ dans la barre de saisie puis tracer la tangente au point d'abscisse 1 en utilisant TANGENTE[1,$f$]
Avec la calculatrice saisir $f$ dans Y1 et l'équation réduite de $T$ dans Y2

Solution

Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION

Inscrivez-vous pour accéder à ce contenu gratuitement!

Ressource précédente: Étude de la convexité d’une fonction avec une exponentielle (réf 1066) Ressource suivante: Étude d’une fonction avec exponentielle (extrait BAC) (réf 1070)

enable JavaScriptChatBot