Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équations de droites et de plans dans un repère de l’espace
Intersections droite plan
Calcul d’un volume
Ressources associées et exercices semblables
Devoir fin de chapitre géométrie dans l’espace dans un repère (réf 1293)
devoir
Devoir deux exercices BAC 2023 volume d’un tétraèdre et d’un cône dans un repère (réf 1294)
devoir
Fiche méthode représentation paramétrique d’une droite (réf 1295)
méthode
On considère le plan $\mathcal{P}$ d'équation $2x + y - 2z + 4 = 0$ et les points $A$ de coordonnées $(3 ; 2 ; 6)$, B de coordonnées $(1 ; 2 ; 4)$, et $C$ de coordonnées $(4;-2;5)$.
- Vérifier que les points A, B et C définissent un plan.
Rappel cours
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $
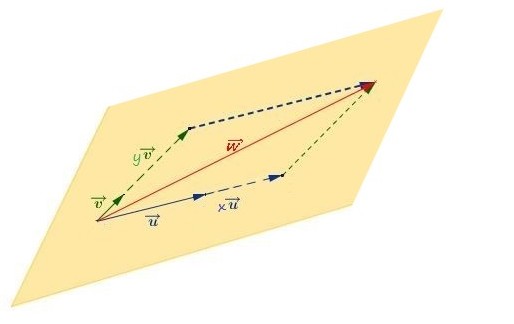
vecteurs coplanaires
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
Aide
Il faut vérifier que les points $A$, $B$ et $C$ ne sont pas alignés donc que les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ ne sont pas colinéaires
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Vérifier que ce plan est le plan $\mathcal{P}$.
Aide
Il faut vérifier que les points $A$, $B$ et $C$ appartiennent à $\mathcal{P}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que le triangle $ABC$ est rectangle.
Rappel cours
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$
Orthogonalité et produit scalaire
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.Aide
Il faut vérifier si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont orthogonaux.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une représentation paramétrique de paramétriques de la droite $\Delta$ passant par l'origine du repère et perpendiculaire
au plan $\mathcal{P}$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Un vecteur normal au plan $\mathcal{P}$ est un vecteur directeur de $\Delta$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer les coordonnées du point d'intersection $H$ de $\Delta$ et de $(ABC)$
Aide
Il faut écrire une équation d'inconnue $t$ en remplaçant dans l'équation de $(ABC)$ les expressions de $x$, $y$ et $z$ données avec la représentation paramétrique de $\Delta$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire le volume du tétraèdre $OABC$.
Rappel cours
Distance dans l'espace
Si le repère de l'espace est orthonormé, la distance $AB$ est: $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$Aide
Il faut calculer les distances $AB$, $AC$ et $OH$
Rappel: $V=\dfrac{\text{Aire de la base}\times \text{hauteur}{3}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère les points $A(0 ; 2 ; 0)$, $B(0 ; 0 ; 6)$, $C(4;0;0)$, $D(0;4;0)$ et $E(0;0;4)$.

- Vérifier que le vecteur $\overrightarrow{n}\begin{pmatrix}
1\\
1\\
1
\end{pmatrix}$ est un vecteur normal au plan $(CDE)$.
Rappel cours
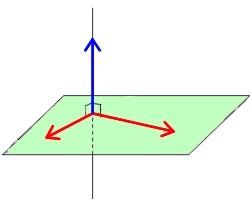
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Aide
Il faut vérifier que le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{CD}$ et $\overrightarrow{CE}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire une équation cartésienne du plan $(CDE)$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Le plan $P$ a pour équation $3y+z-6=0$
Montrer que la droite d'intersection de $P$ et du plan $(OIJ)$ est une droite $d$ passant par $A$ et parallèle à $(OI)$ et que le point $B$ appartient au plan $P$.
Représenter les traces (les droites d'intersection) de $P$ sur les plans de bases du repère.Aide
Si un point $M(x;y;z)$ appartient au plan $(OIJ)$ alors on a $z=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Justifier que les plans $P$ et $(CDE)$ sont sécants.
Aide
Il faut vérifier si les vecteurs normaux des plans $(CDE)$ et $P$ sont colinéaires
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Construire la droite $\Delta$ intersection de $P$ et $(CDE)$ sur le graphique.
Aide
Il faut chercher deux points d'intersectionnde $P$ et $(CDE)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la représentation paramétrique de $\Delta$.
Aide
Les points d'intersection de $P$ et $(CDE)$ vérifient les équations des deux plans.
On peut exprimer $x$ et $z$ en fonction de $y$ par exempleSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Infos abonnements


 Envoyez votre message
Envoyez votre message