Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Deux exercices BAC 2023 spécialité maths
Dérivation, limites, théorème des valeurs intermédiaires et convexité
Ressources associées et exercices semblables
Devoir convexité (réf 1075)
devoir
$\mathcal{T}$ est la tangente à la courbe au point $A(1;1)$
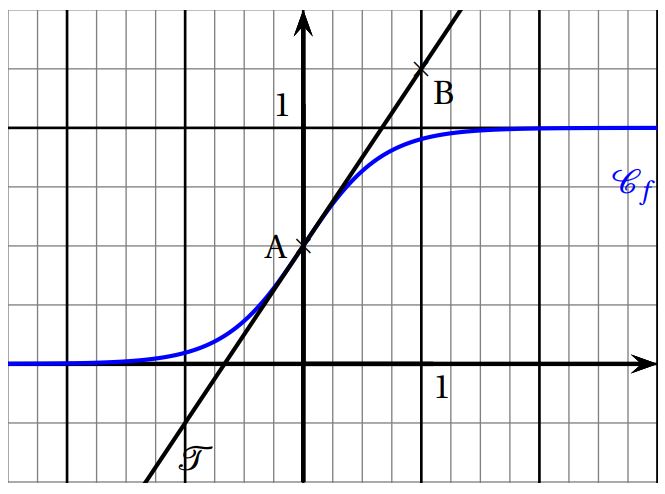
Partie A : lectures graphiques
- Déterminer l'équation réduite de la tangente $\mathcal{T}$.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements- Donner les intervalles sur lesquels la fonction $f$ semble convexe ou concave.
Rappel cours
Convexité et tangentes
Soit $f$ une fonction dérivable sur un intervalle I et $\mathcal{C}_f$ sa courbe représentative.
$f$ est convexe sur I si la courbe $\mathcal{C}_f$ est au-dessus de ses tangentes.
Dans le cas contraire, $\mathcal{C}_f$ en-dessous de ses tangentes), $f$ est concave.Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie B : étude de la fonction- On admet que la fonction $f$ est dérivable sur $\mathbb{R}$.
Déterminer l'expression de sa fonction dérivée $f'$.Rappel cours
Dérivée de $\dfrac{1}{u}$
$\left(\dfrac{1}{u}\right)'=\dfrac{-u'}{u^2}$
Cas de la fonction $e^{u}$
La fonction $f$ définie sur $I$ par $f(x)=e^{u(x)}$ avec $u$ fonction dérivable sur $I$ est dérivable sur $I$ et $f'(x)=u'(x)e^{u(x)}$Aide
On pose $u(x)=1+e^{-3x}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Justifier que la fonction $f$ est strictement croissante sur $\mathbb{R}$.
Aide
$e^{-3x} > 0$ et $\left(1 + e^{- 3x}\right)^2 > 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements -
- Déterminer la limite en $+\infty$ de la fonction $f$.
Aide
On pose $u(x)=e^{-3x}=X$ et on utilise la composée de exponentielle et de $u$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer la limite en $- \infty$ de la fonction $f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Déterminer la limite en $+\infty$ de la fonction $f$.
Partie C : Tangente et convexité- Déterminer par le calcul une équation de la tangente $\mathcal{T}$ à la courbe $\mathcal{C}_f$ au point d'abscisse $0$.
Rappel cours
Équation de la tangente au point d'abscisse $a$
$f$ est une fonction définie et dérivable en $x=a$.
La tangente à $C_f$ en $a$ a pour coefficient directeur $f'(a)$
et pour équation réduite $ y=f'(a)(x-a)+f(a)$}Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On admet que la fonction $f$ est deux fois dérivable sur $\mathbb{R}$.
On note $f''$ la fonction dérivée seconde de la fonction $f$.
On admet que $f''$ est définie sur $\mathbb{R}$ par $f''(x) = \dfrac{9e^{-3x} \left(e^{-3x} - 1\right)}{\left(1 + e^{-3x} \right)^3}$
Étudier le signe de la fonction $f''$ sur $\mathbb{R}$.Aide
e^{-3x} > 0$ et $1+e^{-3x} > 0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements -
- Indiquer, en justifiant, sur quel(s) intervalle(s) la fonction $f$ est convexe.
Rappel cours
Signe de la dérivée seconde
Soit $f$ définie et dérivable sur un intervalle I de $\mathbb{R}$
si $f''(x)>0$ sur $I$ alors $f$ est convexe
si $f''(x)<0$ sur $I$ alors $f$ est concaveSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Que représente le point $A$ pour la courbe $\mathcal{C}_f$ ?
Rappel cours
point d'inflexion et dérivée seconde
si $f"(x)$ s'annule et change de signe en $x=x_A$ alors la courbe admet un point d'inflexion au point $A$.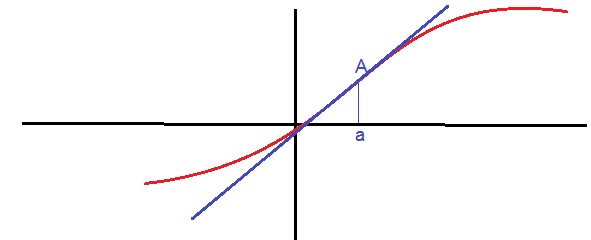
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire la position relative de la tangente $\mathcal{T}$ et de la courbe $\mathcal{C}_f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Indiquer, en justifiant, sur quel(s) intervalle(s) la fonction $f$ est convexe.
Exercice 2 (10 points)Partie A
Le plan est ramené à un repère orthogonal.
On a représenté ci-dessous la courbe d'une fonction $f$ définie et deux fois dérivable sur $\mathbb{R}$, ainsi que celle de sa dérivée $f'$ et de sa dérivée seconde $f''$.
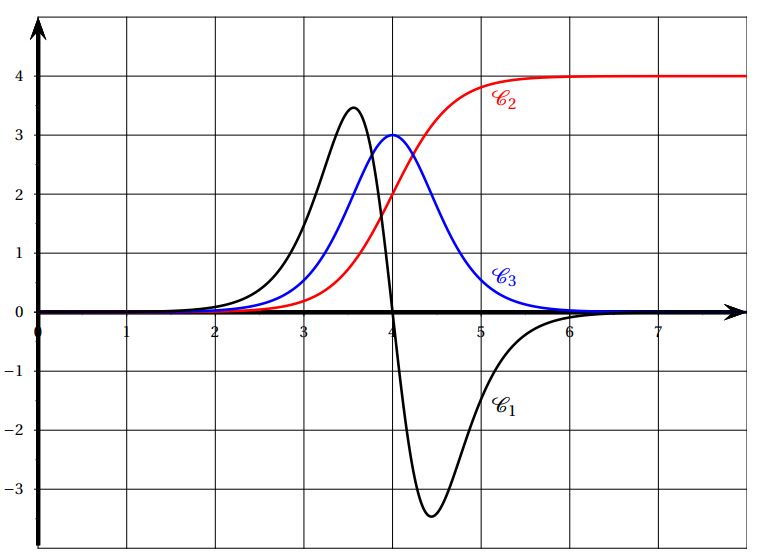
- Déterminer, en justifiant votre choix, quelle courbe correspond à quelle fonction.
Aide
Lorsque $f$ est croissante alors $f'(x) >0$
Lorsque $f$ est convexe alors $f''(x) > 0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer, avec la précision permise par le graphique, le coefficient directeur de la tangente à la courbe $\mathcal{C}_2$ au point d'abscisse $4$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Donner avec la précision permise par le graphique, l'abscisse de chaque point d'inflexion de la courbe $\mathcal{C}_1$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie B
$k$ est un réel strictement positif.
On considère la fonction $g$ définie sur $\mathbb{R}$ par $g(x) = \dfrac{4}{1 + e^{- kx}}$.- Déterminer les limites de $g$ en $+ \infty$ et en $-\infty$
Aide
On pose $u(x)=-kx=X$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Prouver que $g'(0) = k$.
Rappel cours
Cas de la fonction $e^{u}$
La fonction $f$ définie sur $I$ par $f(x)=e^{u(x)}$ avec $u$ fonction dérivable sur $I$ est dérivable sur $I$ et $f'(x)=u'(x)e^{u(x)}$
$\left(\dfrac{1}{u}\right)'=\dfrac{-u'}{u^2}$Aide
On pose $u(x)=1+e^{-kx}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Un logiciel de calcul formel, donne les résultats ci-dessous:

Prouver que la courbe de $g$ admet un point d'inflexion au point d'abscisse 0.Aide
Il faut que la dérivée seconde s'annule et change de signe en $x=0$ donc étudier le signe de g''(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Donner les intervalles sur lesquels la fonction $f$ semble convexe ou concave.


 Envoyez votre message
Envoyez votre message