Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Coordonnées d’un vecteur dans un repère de l’espace
Points et vecteurs coplanaires (combinaison linéaire de deux vecteurs)
Représentation paramétrique d’une droite et intersection de deux droites
Ressources associées et exercices semblables
Droites concourantes dans un repère de l’espace (réf 1283)
exercice
Devoir fin de chapitre géométrie dans l’espace dans un repère (réf 1292)
devoir
Devoir fin de chapitre géométrie dans l’espace dans un repère (réf 1293)
devoir
Produit scalaire, équations de droites et de plans dans un repère de l’espace (réf 1298)
mémo
- Déterminer les coordonnées de $D$ pour que le quadrilatère $ABCD$ soit un parallélogramme.
Rappel cours
Coordonnées d'un vecteur dans l'espace
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
$\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $Aide
Les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{DC}$ doivent avoir les même coordonnées.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Soit $E(2;4;2)$, montrer que le point $E$ n'appartient pas au plan $(ABC)$.
Rappel cours
vecteurs coplanaires
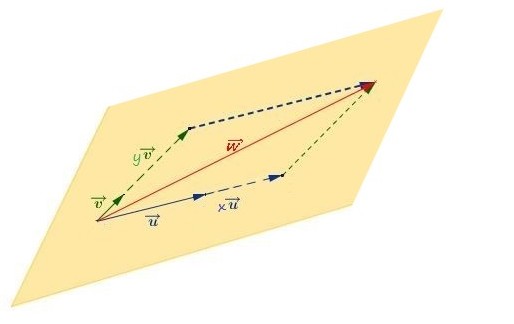
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
Aide
Il faut montrer qu'il n'existe pas de couple de réel $(x;y)$ tel que $\overrightarrow{AE}=x\overrightarrow{AB}+y\overrightarrow{AC}$
Il faut écrire un système d'équations d'inconnues $x$, $y$ et $z$ formé avec les coordonnées des vecteursSolution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Le point $A$ appartient-il à la droite $d$?
Aide
Il faut déterminer la valeur de $t$ en utilisant l'abscisse de $A$ et calculer $y$ puis $z$ avec cette valeur
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une représentation paramétrique de $d'$ parallèle à $d$ et passant par $A$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Un vecteur directeur de $d$ est aussi un vecteur directeur de $d'$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une représentation paramétrique de la droite $(AB)$ avec $B(2; 1;-10 )$
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
$\overrightarrow{AB}$ est un vecteur directeur de $(AB)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Les droites $d$ et $(AB)$ sont-elles sécantes?
Aide
Il faut écrire un système d'équations d'inconnues $t$ et $t'$ formé avec les représentations paramétrique de $d$ et $(AB)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Infos abonnements


 Envoyez votre message
Envoyez votre message