Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Équation d’un plan Représentation paramétrique d’une droite
Intersection droite-plan
Vecteurs orthogonaux et produit scalaire dans l’espace
Ressources associées et exercices semblables
Exercice BAC 2023 droites et plans dans un repère de l’espace (réf 1289)
exercice
Devoir fin de chapitre géométrie dans l’espace dans un repère (réf 1292)
devoir
Devoir fin de chapitre géométrie dans l’espace dans un repère (réf 1293)
devoir
Devoir deux exercices BAC 2023 volume d’un tétraèdre et d’un cône dans un repère (réf 1294)
devoir
Le plan $\mathcal{P}$ a pour équation cartésienne $x + y + 3z + 4 = 0$.
Dire si chacune des affirmations ci-dessous est vraie ou fausse en justifiant la réponse.
- Le point $A(-2;4;-2)$ appartient à $\mathcal{P}$.
Aide
Les coordonnées de $A$ doivent vérifier l'équation de $\mathcal{P}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - La droite $d$ passant par $A$ et $B(1 ;7 ;7 )$ est orthogonale au plan $P$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Un \overrightarrow directeur de $d$ doit être colinéaire à un \overrightarrow normal au plan $P$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On note S le point de coordonnées $(1;-2;- 2)$.
La droite $\Delta$ qui passe par S et qui est perpendiculaire au plan $\mathcal{P}$ a pour représentation paramétrique $\begin{cases} x=2 + t\\ y= - 1 + t\\ z=1 + 3t \end{cases}$ avec $t \in \textbf{R}$.Rappel cours
Représentation paramétrique d'une droite
Dans l'espace muni d'un repère, la droite passant par $A(x_A;y_A;z_A)$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}$ a pour représentation paramétrique $ \begin{cases} x=x_A+tu_1\\ y=y_A+tu_2\\ z=z_A+tu_3 \end{cases}$Aide
Un \overrightarrow normal au plan $\mathcal{P}$ est aussi un \overrightarrow directeur de $\Delta$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
On considère le cube $ ABCDEFGH$, d'arête de longueur 1, représenté ci-dessous et on munit l'espace du repère orthonormé $\left(A;\overrightarrow{AB}; \overrightarrow{AD};\overrightarrow{AE}\right)$.

- Déterminer une représentation paramétrique de la droite $(FD)$.
Rappel cours
Représentation paramétrique d'une droite
Dans l'espace muni d'un repère, la droite passant par $A(x_A;y_A;z_A)$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}$ a pour représentation paramétrique $ \begin{cases} x=x_A+tu_1\\ y=y_A+tu_2\\ z=z_A+tu_3 \end{cases}$Aide
Dans le repère $F(1;0;1)$ et $D(0;1;0)$ et $\overrightarrow{FD}$ est un vecteur directeur de de $(FD)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Démontrer que le $ \overrightarrow{n}\begin{pmatrix}1\\- 1\\1\end{pmatrix}$ est un vecteur normal au plan $(BGE)$ et déterminer une équation du plan $(BGE)$.
Rappel cours
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Aide
Il faut vérifier que le vecteur $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{BG}$ et $\overrightarrow{BE}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que la droite $(FD)$ est perpendiculaire au plan $(BGE)$ en un point $K$ de coordonnées $K\left(\frac{2}{3};\frac{1}{3};\frac{2}{3}\right)$.
Rappel cours
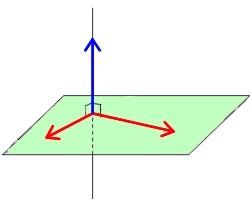
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
Aide
es vecteurs directeurs de $(FD)$ doivent être colinéaire à un vecteur normal du plan $(BGE)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Quelle est la nature du triangle $BEG$ ? Déterminer son aire.
Aide
Les côtés du triangle sont les diagonales des faces du cube
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire le volume du tétraèdre $BEGD$.
Aide
$(FD)$ est orthogonale au plan $(BGE)$ donc $K$ est le projeté orthogonal de $D$ sur $(BGE)$
Rappel: $V=\dfrac{\text{aire de la base}\times \text{hauteur}}{3}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Soit $ABCDEFGH$ un parallélépipède rectangle tel que $AB = 2$, $AD = 3$ et $AE = 1$.
On appelle respectivement $I$, $J$ et $P$ les milieux respectifs des segments $[CD]$, $[EF]$ et $[AB]$.
On note $Q$ le point défini par $\overrightarrow{AQ}= \dfrac{1}{3}\overrightarrow{AD}$.

On appelle plan médiateur d'un segment le plan perpendiculaire à ce segment et passant par son milieu.
L'objectif de l'exercice est de déterminer les coordonnées du centre d'une sphère circonscrite au tétraèdre $ABIJ$ (c'est-à-dire une sphère qui passe par les quatre points $A$, $B$, $I$, $J$).
L'espace est rapporté au repère orthonormal $\left(A;\overrightarrow{AP},\overrightarrow{AQ},\overrightarrow{AE}\right)$. \medskip
- Justifier que les quatre points $A$, $B$, $I$ et $J$ ne sont pas coplanaires.
Rappel cours
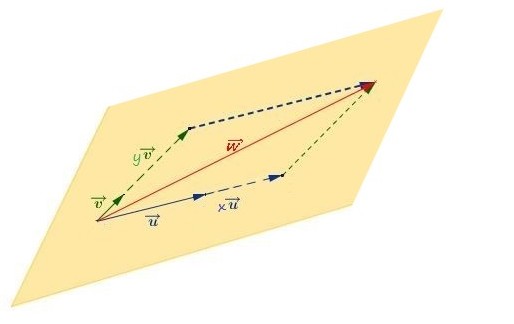
vecteurs coplanaires
Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.
Aide
$I$ milieu de $[CD]$ donc $I$ appartient au plan $(ABD)$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une équation cartésienne du plan médiateur
$\left(P_{1}\right)$ du segment $[AB]$.
Rappel cours
010 Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
010 $\left(P_{1}\right)$ est orthogonal à la droite $(AB)$ donc $\overrightarrow{AB}$ est un vecteur normal au plan $\left(P_{1}\right)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Soit $\left(P_{2}\right)$ le plan d'équation cartésienne $3y - z - 4 = 0$.
Montrer que le plan $\left(P_{2}\right)$ est le plan médiateur du segment $[IJ]$.Rappel cours
011 Coordonnées du milieu
L'espace est muni d'un repère quelconque.
Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$ Le milieu $I$ de $[AB]$ a pour coordonnées $\left(\dfrac{x_A+x_B}{2};\dfrac{y_A+y_B}{2};\dfrac{z_A+z_B}{2}\right)$Aide
011 Il faut montrer que le vecteur $\overrightarrow{IJ}$ est colinéaire à un vecteur directeur de $ \left(P_{2}\right)$ et que le milieu de $[IJ]$ appartient à $\left(P_{2}\right)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements -
- Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
Aide
012 Les deux plans sont sécants si leurs vecteurs normaux sont colinéaires
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que leur intersection est une droite $(\Delta)$ dont une représentation paramétrique est
$\begin{cases}
x= 1\\
y = t\\
z = 3t - 4
\end{cases}$ avec $t\in \mathbb{R}$
Aide
013 On peut exprimer $x$ et $y$ en fonction de $z$ par exemple en utilisant les équations des deux plans
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer les coordonnées du point $\Omega$ de la droite $(\Delta)$ tel que $\Omega A = \Omega I$.
Rappel cours
014 Distance dans l'espace
Si le repère de l'espace est orthonormé, la distance $AB$ est: $AB=\sqrt{(x_B-x_A)^2+(y_B-y_A)^2+(z_B-z_A)^2}$Aide
014 Il faut écrire une équation d'inconnue $t$ avec les coordonnées de $\Omega$ exprimées en fonction de $t$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que le point $\Omega$ est centre de la sphère circonscrite au tétraèdre $ABIJ$.
Aide
015 Il faut vérifier que $\Omega A=\Omega B=\Omega I=\Omega J$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Démontrer que les plans $\left(P_{1}\right)$ et $\left(P_{2}\right)$ sont sécants.
Infos abonnements


 Envoyez votre message
Envoyez votre message