Informations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Aire du domaine sous la courbe avec une fonction de signe non constant
Étude des variations et limites d’une fonction avec ln
Intégration par parties
Suite définie par une intégrale
Ressources associées et exercices semblables
- Déterminer le signe de $f$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer l'aire $A$, en unités d'aire, du domaine limité par la courbe $\mathcal{C}_f$, l'axe des abscisses et les droites d'équations $x=0$ et $x=3$.
Rappel cours
Aire sous la courbe
Soit $f$ une fonction continue sur $[a;b]$, l'aire du domaine limité par la courbe, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$ est:
$\displaystyle \int_a^b f(x)dx$ si $f$ est positive sur $[a;b]$
$-\displaystyle \int_a^b f(x)dx$ si $f$ est négative sur $[a;b]$Aide
Il faut distinguer les intervalles $[0;2]$ et $[2;3]$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
La représentation graphique $C_f$ de $f$ est donnée ci-dessous.

- Déterminer la limite de $f$ en $0$ et en donner une interprétation graphique.
Rappel cours
Limites de ln
$\displaystyle \lim_{x \rightarrow 0^+}ln(x)=-\infty$
$\displaystyle \lim_{x \rightarrow +\infty}ln(x)=+\infty$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $f'(x)$ et dresser le tableau de variation de $f$.
Rappel cours
Dérivée de la fonction ln
La fonction $ln$ est dérivable sur $]0;+\infty[$ et $(ln(x))'=\dfrac{1}{x}$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Justifier que l'équation $f(x)=0$ admet sur $[2;5]$ une unique solution $\alpha$ et en donner une valeur approchée aux centièmes par défaut.
Rappel cours
Théorème des valeurs intermédiaires
$f$ est une fonction continue sur $[a;b]$ (avec $a < b$).
Si $k$ est un réel compris entre $f(a)$ et $f(b)$ alors il existe au moins un réel $c\in [a;b]$ tel que $f(c)=k$.
Cas où la fonction est monotone
Si $f$ est continue sur $[a;b]$ et strictement monotone alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$ l'équation $f(x)=k$ admet une unique solution.
$f$ strictement monotone signifie que $f$ est strictement croissante (ou strictement décroissante).Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements -
- Calculer $f(1)$.
Aide
rappel $ln(1)=0$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire le signe de $f(x)$
Aide
Lorsque $f(x)=0$ la courbe coupe l'axe des abscisses
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En utilisant une intégration par parties, calculer $\displaystyle \int_1^\alpha ln(x)dx$ en fonction de $\alpha$.
Rappel cours
Intégration par parties
$u$ et $v$ sont deux fonctions dérivables sur $[1;b]$.
$\displaystyle \int_a^b u'v=[uv]_a^b-\int_a^b uv'$Aide
On pose $u'(x)=1$ et $v(x)=ln(x)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - On note $\mathcal{A}$ l'aire, en unités d'aires, du domaine limité par la courbe et l'axe des abscisses.
Hachurer la zone correspondant à cette aire sur le graphique et calculer cette aire en fonction de $\alpha$ et en donner une valeur arrondie aux dixièmes en prenant $\alpha \approx 3,51$.Rappel cours
Aire et intégrale
$f$ est une fonction continue et positive sur $[a;b]$ avec $a < b$.
$\int_a^b f(x)dx$ est l'aire, en unités d'aires, du domaine limité par la courbe de $f$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$.
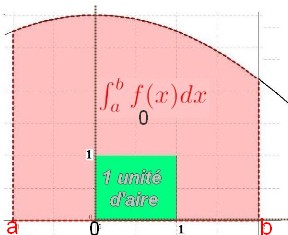
Intégrale
La fonction $f$ est continue sur $[ab]$ et $F$ est une primitive de $f$ sur $[a;b]$
$\int_a^b f(x)dx=[F(x)]_a^b=F(b)-F(a)$Aide
Utiliser le signe de $f(x)$ et le résultat de $\displaystyle \int_1^\alpha ln(x)dx$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
- Calculer $f(1)$.
- Calculer $I_0$.
Rappel cours
Primitives des fonctions usuelles
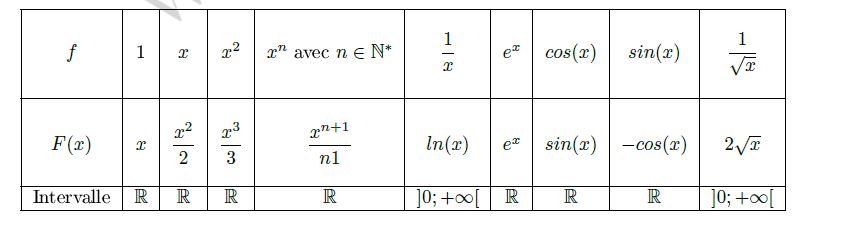
Aide
Pour $n=0$ il faut chercher une primitive de $e^x$ car $x^0=1$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que la suite $(I_n)$ est décroissante.
Rappel cours
Étude des variations(différence de deux termes consécutifs)
Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
Exprimer $u_{n+1}-u_n$ en fonction de $n$
Étudier le signe de l'expression obtenue
Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante. inlcude236fcludeAide
On peut étudier le signe de $I_{n+1}-I_n$
Si $f$ est positive sur $[a;b]$ avec $a < b$ alors $\int_a^b f(x)dx>0$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message