Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Produit scalaire dans un repère de l’espace et vecteurs orthogonaux
Droite orthogonale à un plan dans un cube
Ressources associées et exercices semblables
Équation d’un plan orthogonal à une droite (réf 1279)
exercice
Exercice bilan équation d’un plan et intersection droite-plan (réf 1280)
exercice
Vidéo de l’exercice

Partie 1 Sans utiliser de repère
- Calculer $\overrightarrow{EG}.\overrightarrow{FD}$.
Rappel cours
relation de Chasles
$\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ Orthogonalité et produit scalaire
Pour tous vecteurs $\overrightarrow{u}$ et $\overrightarrow{v}$, on a:
$\overrightarrow{u}.\overrightarrow{v}=0 \Longleftrightarrow \overrightarrow{u}=\overrightarrow{0}$ ou $\overrightarrow{v}=\overrightarrow{0}$ ou $\overrightarrow{u}$ et $\overrightarrow{v}$ sont orthogonaux.Aide
$\overrightarrow{FD}=\overrightarrow{FH}+\overrightarrow{HD}$ et $\overrightarrow{EG}=\overrightarrow{EF}+\overrightarrow{FG}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Calculer $\overrightarrow{EB}.\overrightarrow{FD}$.
Aide
$\overrightarrow{EB}=\overrightarrow{EF}+\overrightarrow{FD}$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire que le plan $(EBG)$ est perpendiculaire à la droite $(FD)$.
Rappel cours
droite et plan orthogonaux
Une droite $(d)$ est orthogonale à un plan si et seulement si un vecteur directeur de $(d)$ est orthogonal à deux vecteurs directeurs de du plan.
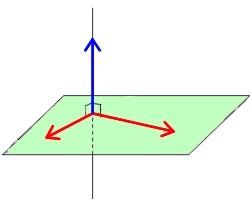
Aide
Il faut justifier que $(FD)$ est orthogonale à deux droites sécantes du plan $(EBG)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements
Partie 2: En utilisant un repère orthonormé
On considère le repère orthonormé $(A;\overrightarrow{AB};\overrightarrow{AD};\overrightarrow{AE})$.
Retrouver les résultats des questions 1 et 2 de la partie A et conclure.
Rappel cours
Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix}
x\\
y\\
z
\end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix}
x'\\
y'\\
z'
\end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message