Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Fonction associée à une suite
Dérivée d’une fonction
Étude des variations avec la fonction associée
Ressources associées et exercices semblables
Variations d’une suite définie sous forme explicite (réf 0908)
exercice
Variations d’une suite définie par récurrence (réf 0909)
exercice
- $u_{n}=2n^2+3n-5$
Rappel cours
Variations fonction polynôme du second degré
Soit la fonction $P$ définie sur $\mathbb{R}$ par sa forme canonique $P (x) = a(x-\alpha)^2 + \beta$
La courbe représentative de $P$ est une parabole dont le sommet a pour coordonnées $(\alpha; \beta)$.
Tableau de variation: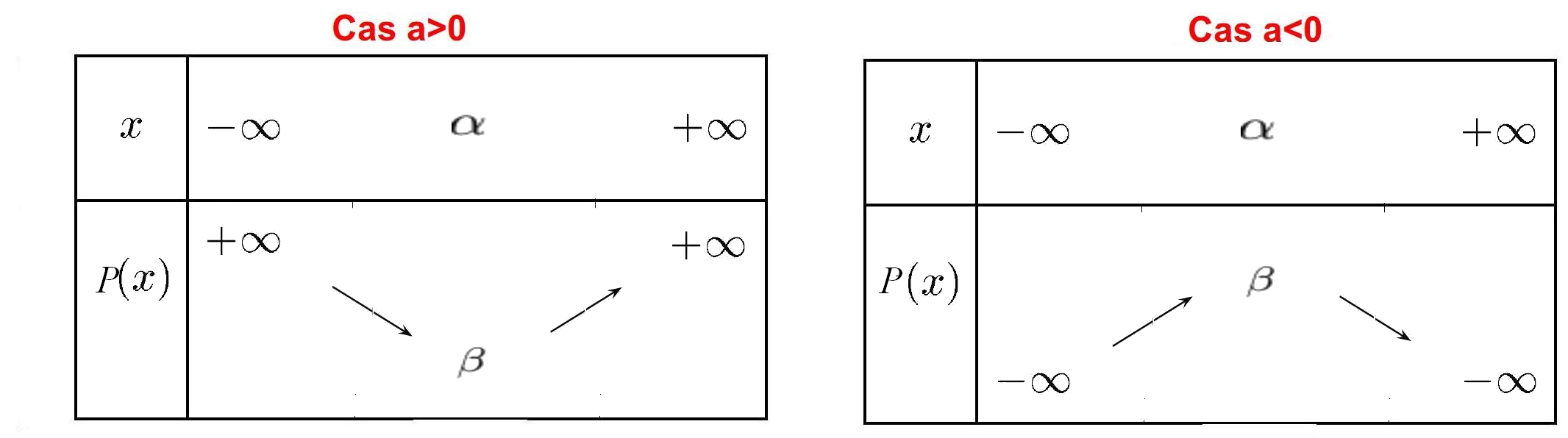
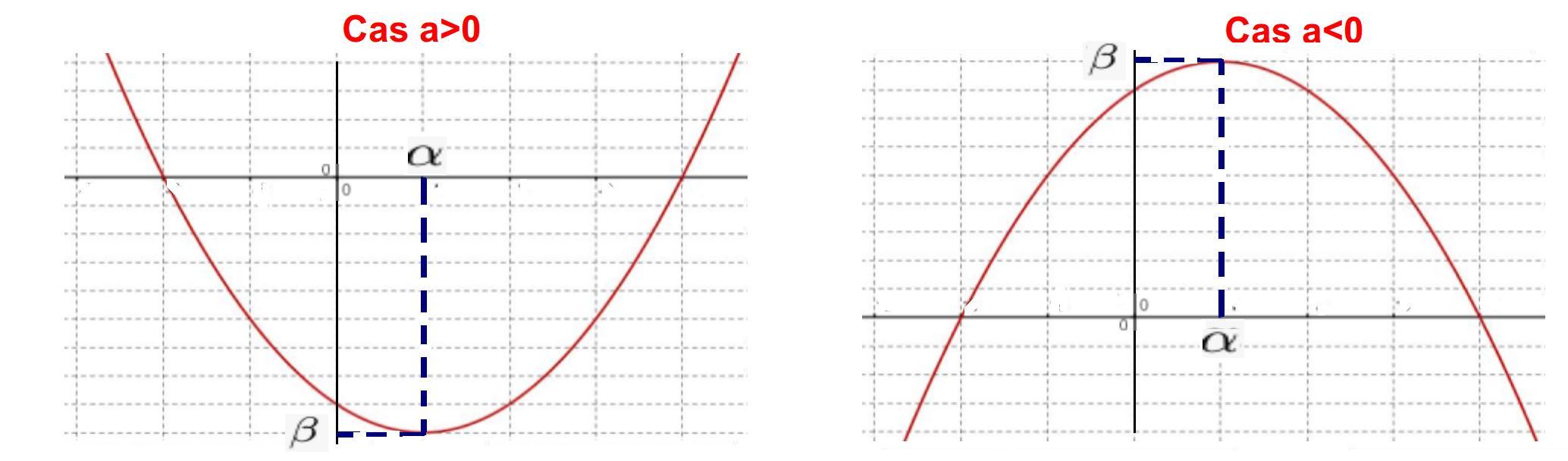
Aide
On peut chercher l'abscisse du sommet puis les variations de la fonction associée à $(u_n)$
Solution
On pose $f$ définie sur $[0;+\infty[$ par $f(x)=2x^2+3x-5$.
On a alors $u_n=f(n)=2n^2-3n-5$ et $f$ est la fonction associée à la suite $(u_n)$. Le sommet de la parabole a pour abscisse $\alpha=\dfrac{-b}{2a}=\dfrac{-3}{4}$
Le coefficient $a=2$ de $x^2$ est positif (parabole à l'endroit)
donc $f$ est croissante pour $x\geq \dfrac{-3}{4}$ donc sur $[0;+\infty[$
Remarque
Si le chapitre dérivation a été traité:
$f$ est dérivable sur $[0;+\infty[$ (fonction polynôme du second degré).
$f'(x)=2\times 2x+3=4x+3$
$x \geq 0$ donc $4x+3 >0$ et $f'(x) >0$
donc $f$ est strictement croissante sur $[0;+\infty[$
- $u_{n}=\dfrac{-2}{n+1}$
Aide
Il faut étudier le signe de la dérivée de $f$ définie sur $[0;+\infty[$ telle que $u_n=f(n)$.
$f(x)=-2\times \dfrac{1}{x+1}$ (formule de dérivation $\dfrac{1}{v}$)Solution
On pose $f$ définie sur $[0;+\infty[$ par $f(x)=\frac{-2}{x+1}$.
On a alors $u_n=f(n)=\dfrac{-2}{n+1}$ et $f$ est la fonction associée à la suite $(u_n)$.
$f$ est dérivable sur $[0;+\infty[$ (quotient de fonctions dérivables).
$f(x)=-2\times \dfrac{1}{x+1}$
On pose $v(x)=x+1$ et on a $v'(x)=1$
$f'(x)=-2\times \dfrac{-v'(x)}{(v(x))^2}$
$\phantom{f'(x)}=-2\times \dfrac{-1}{(x+1)^2}$
$\phantom{f'(x)}= \dfrac{2}{(x+1)^2}$
$(x+1)^2 >0$ donc $f'(x) >0$
donc $f$ est strictement croissante sur $[0;+\infty[$
- $u_{n}=\dfrac{1-n}{n+2}$
Aide
Il faut étudier le signe de la dérivée de $f$ définie sur $[0;+\infty[$ telle que $u_n=f(n)$.
Pour dériver $f$, on pose $u(x)=1-x$ et $v(x)=x+2$Solution
On pose $f$ définie sur $[0;+\infty[$ par $f(x)=\dfrac{1-x}{x+2}$.
On a alors $u_n=f(n)=\dfrac{1-n}{n+2}$ et $f$ est la fonction associée à la suite $(u_n)$.
$f$ est dérivable sur $[0;+\infty[$ (quotient de fonctions dérivables).
On pose $u(x)=1-x$ et $v(x)=x+2$
et on a $u'(x)=-1$ et $v'(x)=1$
$f'(x)=\dfrac{u'(x)v(x)-u(x)v'(x)}{(v(x))^2}$
$\phantom{f'(x)}=\dfrac{-1\times (x+2)-(1-x)}{(x+2 )^2}$
$\phantom{f'(x)}=\dfrac{-x-2-1+x}{(x+2 )^2}$
$\phantom{f'(x)}=\dfrac{-3}{(x+2 )^2}$
$(x+2)^2 >0$ donc $f'(x) < 0$
donc $f$ est strictement décroissante sur $[0;+\infty[$


 Envoyez votre message
Envoyez votre message