Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Exercice BAC spécialité maths 2024
Calculs d’intégrales avec exponentielle
Approximation d’une aire sous la courbe
Intégration par parties
Étude d’une fonction avec exponentielle
Valeur moyenne d’une fonction
Ressources associées et exercices semblables
Vidéo de l’exercice
On a représenté, ci-dessous, la courbe de la température en degrés Celsius à l'intérieur du foyer en fonction du temps écoulé, exprimé en minutes, depuis l'allumage du foyer.
Partie 1 : appareil de la marque A

Par lecture graphique :
- Donner le temps au bout duquel la température maximale est atteinte à l'intérieur du foyer.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Donner une valeur approchée, en minutes, de la durée pendant laquelle la température à l'intérieur du foyer dépasse $300$ degrés Celsius.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - On note $f$ la fonction représentée sur le graphique.
Estimer la valeur de $\displaystyle\dfrac{1}{600} \int_{0}^{600} f(t) dt$ et interpréter le résultat.Rappel cours
Aire et intégrale
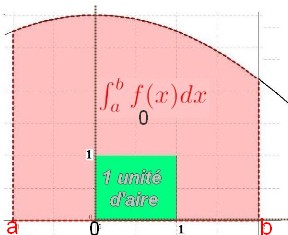
$f$ est une fonction continue et positive sur $[a;b]$ avec $a < b$.
$\int_a^b f(x)dx$ est l'aire, en unités d'aires, du domaine limité par la courbe de $f$, l'axe des abscisses et les droites d'équations $x=a$ et $x=b$.
Valeur moyenne
$f$ est continue sur $[a;b]$.
La valeur moyenne de $f$ sur $[a;b]$ est $M=\dfrac{1}{b-a}\displaystyle \int_a^b f(x)dx$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Partie 2 : étude d'une fonction
Soit la fonction $g$ définie sur l'intervalle $[0~;~+ \infty[ $ par $g(t) = 10 t e^{-0,01 t} + 20$.
- Déterminer la limite de $g$ en $+ \infty$.
Rappel cours
Croissances comparées de $x^n$ et $e^x$
$n\in \mathbb{N}^*$
$\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{e^x}{x^n}=+\infty$Aide
On a $g(t)=-1000\times (-0,01t)e^{-0,01t}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION -
- Montrer que pour tout $t \in [0~;~+ \infty[$, on a $g'(t)=(-0,1 t + 10) e^{- 0,01 t}$.
Aide
On pose $u(t)=10 t $ et $v(t)=e^{-0,01t}$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Étudier les variations de la fonction $g$ sur $[0~;~+ \infty[$ et construire son tableau de variations.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
- Montrer que pour tout $t \in [0~;~+ \infty[$, on a $g'(t)=(-0,1 t + 10) e^{- 0,01 t}$.
- Démontrer que l'équation $g(t) = 300$ admet exactement deux solutions distinctes sur [$0~;~+ \infty[$.
En donner des valeurs approchées à l'unité.Rappel cours
Théorème des valeurs intermédiaires
$f$ est une fonction continue sur $[a;b]$ (avec $a < b$).
Si $k$ est un réel compris entre $f(a)$ et $f(b)$ alors il existe au moins un réel $c\in [a;b]$ tel que $f(c)=k$.
Cas où la fonction est monotone
Si $f$ est continue sur $[a;b]$ et strictement monotone alors pour tout réel $k$ compris entre $f(a)$ et $f(b)$ l'équation $f(x)=k$ admet une unique solution.
$f$ strictement monotone signifie que $f$ est strictement croissante (ou strictement décroissante).Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - À l'aide d'une intégration par parties, calculer $\displaystyle \int_{0}^{600} g(t)dt$.
Rappel cours
Intégration par parties
$u$ et $v$ sont deux fonctions dérivables sur $[1;b]$.
$\displaystyle \int_a^b u'v=[uv]_a^b-\int_a^b uv'$Aide
Utiliser la linéarité pour décomposer en deux intégrales
On pose $u(t) = t$ et $v'(t) = e^{-0,01t}$.Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION
Partie 3 : évaluation
Pour un appareil de la marque B, la température en degrés Celsius à l'intérieur du foyer $t$ minutes après l'allumage est modélisée sur $[0~;~600]$ par la fonction $g$.
L'organisme certificateur attribue une étoile par critère validé parmi les quatre suivants :
- Critère 1 : la température maximale est supérieure à $320~$ degrés celsius
- Critère 2 : la température maximale est atteinte en moins de 2 heures.
- Critère 3 : la température moyenne durant les 10 premières heures après l'allumage dépasse $250$ degrés celsius
- Critère 4 : la température à l'intérieur du foyer ne doit pas dépasser $300$ degrés celsius pendant plus de 5 heures.
Chaque appareil obtient-il exactement trois étoiles ? Justifier votre réponse.
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message