Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Exercice BAC spécialité maths
Géométrie dans l’espace dans un repère orthonormé
Équation d’un plan et d’une droite
Intersections de droites et de plans
Ressources associées et exercices semblables
Exercice BAC droites et plans dans un repère de l’espace (réf 1284)
exercice
Exercice BAC droites et plans dans un repère de l’espace (réf 1285)
exercice
Exercice BAC 2023 droites et plans dans un repère de l’espace (réf 1289)
exercice
Devoir deux exercices BAC 2023 volume d’un tétraèdre et d’un cône dans un repère (réf 1294)
devoir
Vidéo de l’exercice
$I$, $J$ et $K$ sont les points tels que $\overrightarrow{AI} = \dfrac{1}{2} \overrightarrow{AB}$, $\overrightarrow{BJ} = \dfrac{2}{5} \overrightarrow{BC}$, $\overrightarrow{BK} = \dfrac{2}{7} \overrightarrow{BF}$.
On se place dans le repère $\left(B; \overrightarrow{BI}, \overrightarrow{BJ},\overrightarrow{BK}\right)$.
- Quelle est la nature du repère $\left(B; \overrightarrow{BI}, \overrightarrow{BJ},\overrightarrow{BK}\right)$?
Aide
Il faut vérifier que les axes du repère sont orthogonaux deux à deux et que $BI=BJ=BK$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Vérifier que le vecteur $\overrightarrow{n}$ de coordonnées $\begin{pmatrix}2\\2\\- \dfrac{18}{7}\end{pmatrix}$ est normal au plan $(IJH)$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$ Produit scalaire dans un repère orthonormé de l'espace
Dans un repère orthonormé de l'espace, on a les vecteurs $\overrightarrow{u}\begin{pmatrix} x\\ y\\ z \end{pmatrix}$ et $\overrightarrow{v}\begin{pmatrix} x'\\ y'\\ z' \end{pmatrix}$.
$\overrightarrow{u}.\overrightarrow{v}=xx'+yy'+zz'$Aide
Il faut vérifier que le vecteur normal $\overrightarrow{n}$ est orthogonal aux vecteurs $\overrightarrow{IJ}$ et $\overrightarrow{IH}$
$I(1;0;0)$, $J(0;1;0)$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire une équation cartésienne du plan $(IJH)$.
Rappel cours
Vecteur normal à un plan-équation cartésienne d'un plan
Dans l'espace muni d'un repère othonormé, $P$ est un plan de l'espace, un vecteur $\overrightarrow{n}$ normal à $P$ est un vecteur directeur d'une droite orthogonale à $P$.
Le vecteur $\overrightarrow{n}$ est un vecteur normal au plan $P$ passant par $A$ et $P$ est l'ensemble des points $M(x;y;z)$ vérifiant $\overrightarrow{AM}.\overrightarrow{n}=0$.
$ax+by+cz+d=0$ est une équation cartésienne de $P$ de vecteur normal $\overrightarrow{n}\begin{pmatrix} a\\ b\\ c \end{pmatrix}$Aide
Les coefficients de $x$, $y$ et $z$ dans $ax+by+cz+d=0$ sont donnés par les coordonnées d'un vecteur normal au plan $(IJH)$ et on détermine $d$ en utilisant les coordonnées du point $I$ par exemple
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Déterminer une représentation paramétrique de la droite $(CG)$ et en déduire les coordonnées du point d'intersection $M$ du plan $(IJH)$ et de la droite $(CG)$ .
Rappel cours
Représentation paramétrique d'une droite
Dans l'espace muni d'un repère, la droite passant par $A(x_A;y_A;z_A)$ et de vecteur directeur $\overrightarrow{u}\begin{pmatrix}u_1\\u_2\\u_3\end{pmatrix}$ a pour représentation paramétrique $ \begin{cases} x=x_A+tu_1\\ y=y_A+tu_2\\ z=z_A+tu_3 \end{cases}$Aide
$\overrightarrow{CG}=\dfrac{7}{2}\overrightarrow{BK}$ donc $\overrightarrow{BK}$ est un vecteur directeur de $(CG)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Tracer la section du pavé $ABCDEFGH$ par le plan $(IJH)$ en utilisant le point $M$.
Ce tracé sera réalisé sur la figure.Rappel cours
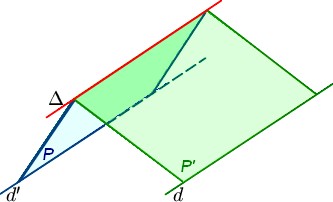
théorème du toit
Lorsque deux plans $P$ et $P'$ sont sécants et contiennent respectivement les droites $d$ et $d'$, l'intersection de $P$ et de $P'$ est une droite $\Delta$ parallèle à $d$ et à $d'$.
Aide
Il faut déterminer les intersections plan $(IJH)$ avec chacune des faces du pavé.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements


 Envoyez votre message
Envoyez votre message