Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Conjecturer une limite
Démontrer une limite en l’infini et en un point avec les définitions
Ressources associées et exercices semblables
Démontrer une limite infinie en l’infini (réf 0976)
exercice
Démontrer une limite en l’infini et en un point (réf 0977)
exercice
Vidéo de l’exercice
- Conjecturer (donner sans justifier) $\displaystyle \lim_{x \rightarrow 0^+}f(x)$
Aide
On veut savoir ce qui se passe pour $f(x)$ quand $x \longrightarrow 0^+$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Démontrer cette limite.
Rappel cours
Limite infinie quand $x \longrightarrow a$
$f$ est définie sur un intervalle $I$ contenant $a$.
$\displaystyle \lim_{x \rightarrow a}f(x)=+\infty$ si pour tout réel $A>0$, il existe un réel $\epsilon>0$ avec $]a-\epsilon;a+\epsilon[\subset I$ tel que $f(x)>A$ pour tout $x\in ]a-\epsilon;a+\epsilon[$.
La droite d'équation $x=a$ est asymptote à a courbe.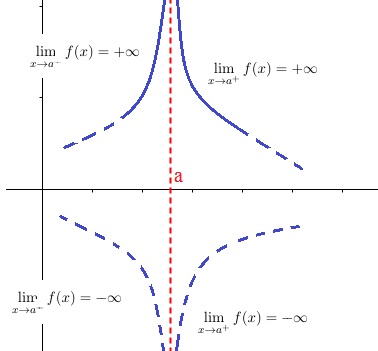
Aide
On veut montrer que pour tout $A >0$, il existe un réel $X_0$ tel que pour tout $0 < x < X_0$ on ait $f(x) > A$
Autrement dit, on veut savoir s'il est possible de rendre $f(x)$ aussi grand que l'on veut quand $x$ est "proche" de zéro.Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Conjecturer (donner sans justifier) $\displaystyle \lim_{x \rightarrow +\infty}f(x)$
Aide
Quand $x\longrightarrow +\infty$ alors le dénominateur est très grand.
On veut savoir ce qui se passe pour $f(x)$ quand $x \longrightarrow +\infty$Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - Démontrer cette limite.
Rappel cours
limite $l$ en $+\infty$ et interprétation graphique
La fonction $f$ est définie sur un intervalle $[a;+\infty[$ et $\ell \in \mathbb{R}$.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)=\ell$ si pour tout intervalle ouvert I contenant $\ell$, il existe $x_0$ tel que pour tout $x>x_0$ on a $f(x)\in $ I
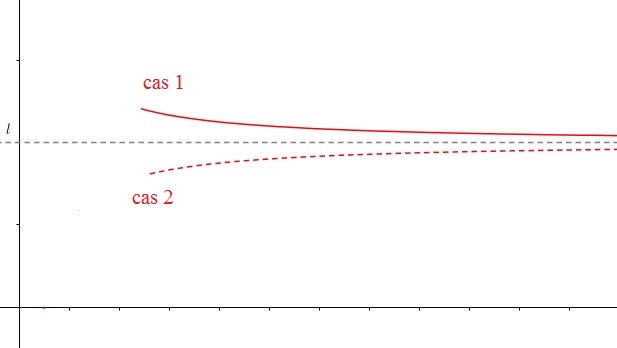
La droite d'équation $y=\ell$ est asymptote à la courbe en $+\infty$Aide
On veut montrer que pour tout $\varepsilon >0$, il existe un réel $X_0$ tel que pour tout $x> X_0$ on ait $-\varepsilon < f(x) < \varepsilon $
Autrement dit, on veut savoir s'il est possible de rendre $f(x)$ aussi "proche" de 0 que l'on veut quand $x$ devient très grand.Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION


 Envoyez votre message
Envoyez votre message