Infos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
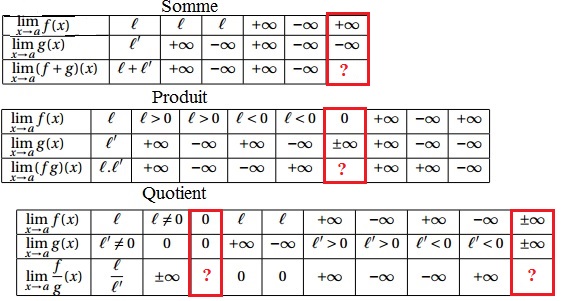
Limite d’une somme
Limite d’un produit
Limite d’un quotient
Ressources associées et exercices semblables
Limite d’une somme, d’un produit et d’un quotient (réf 0985)
exercice
Limites usuelles et opérations sur les limites (réf 0987)
exercice
- $\displaystyle \lim_{x \rightarrow +\infty}f(x)=1$
et $\displaystyle \lim_{x \rightarrow +\infty}g(x)=+\infty$Rappel cours
Opérations sur les limites
Aide
Utiliser les résultats des limites pour une somme, un produit et un quotient.
Il faut essayer de déterminer ces limites de manière "intuitive" sans nécessairement connaître tous les résultats.
Il faut par contre connaître les cas d'indétermination.Solution
Par somme, on a $\displaystyle \lim_{x \rightarrow +\infty}f(x)+g(x)=+\infty$
Par produit $\displaystyle \lim_{x \rightarrow +\infty}f(x)g(x)=+\infty$
Par quotient $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{f(x)}=1$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{f(x)}{g(x)}=0$
Remarque
On peut retrouver les résultats du cours en raisonnant ainsi:
Par exemple pour la somme, on ajoute $f(x)$ proche de 1 avec $g(x)$ infiniment grand...
Pour le quotient, on divise $f(x)$ proche de 1 par un nombre $g(x)$ très grand... - $\displaystyle \lim_{x \rightarrow +\infty}f(x)=0^+$
et $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$Rappel cours
Cas d'indétermination
$+\infty-\infty$
$0\times \pm \infty$
$\dfrac{\pm \infty}{\pm \infty}$
$\dfrac{0}{0}$
Attention, les écritures ci-dessus remplacent les limites mais sont incorrectes...Solution
Par somme, on a $\displaystyle \lim_{x \rightarrow +\infty}f(x)+g(x)=-\infty$
$\displaystyle \lim_{x \rightarrow +\infty}f(x)g(x)$ est indéterminée.
Par quotient $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{f(x)}=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{f(x)}{g(x)}=0$ - $\displaystyle \lim_{x \rightarrow +\infty}f(x)=+\infty$
et $\displaystyle \lim_{x \rightarrow +\infty}g(x)=-\infty$Solution
Par somme, $\displaystyle \lim_{x \rightarrow +\infty}f(x)+g(x)$ est indéterminée.
$\displaystyle \lim_{x \rightarrow +\infty}f(x)g(x)=-\infty$
Par quotient $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{1}{f(x)}=0$
et $\displaystyle \lim_{x \rightarrow +\infty}\dfrac{f(x)}{g(x)}$ est indéterminée.


 Envoyez votre message
Envoyez votre message