Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Limite d’une somme ou d’un quotient utilisant une suite géométrique
Limite d’une suite géométrique dont la raison est comprise entre -1 et 1
Ressources associées et exercices semblables
Limite d’une suite géométrique (réf 0949)
exercice
- $u_n=3\times 0,5^n+4$
Rappel cours
Forme explicite d'une suite géométrique
Si $(u_n)$ est géométrique de raison $q$ est premier terme $u_0$, on a:
$u_n=u_0\times q^n$
et pour tous entiers $n$ et $p$, $u_n=u_p\times q^{n-p}$
Limite de $q^n$ (suite géométrique)
Si $q > 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=+\infty$
Si $-1 < q < 1 $ alors $\displaystyle \lim_{n \rightarrow +\infty}q^n=0$Aide
Déterminer d'abord $\displaystyle \lim_{n \rightarrow +\infty}3\times 0,5^n$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $u_n=\dfrac{2}{3\times 0,4^n}$
Rappel cours
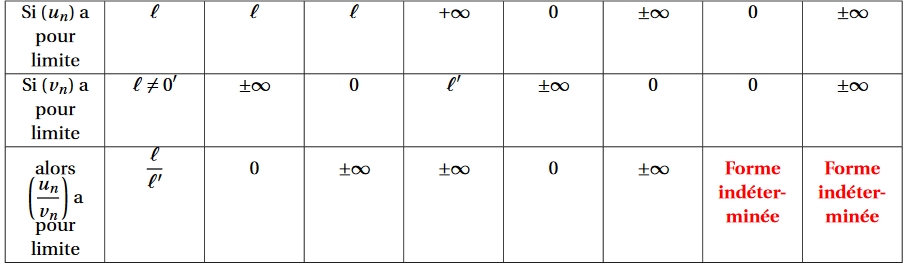
Limite d'un quotient
Aide
Déterminer d'abord $\displaystyle \lim_{n \rightarrow +\infty}3\times 0,4^n$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION - $u_n=\dfrac{\left(\dfrac{1}{3}\right)^n+2}{n}$
Aide
Déterminer d'abord $\displaystyle \lim_{n \rightarrow +\infty}\left(\dfrac{1}{3}\right)^n$
Solution
Vous devez être inscrit pour accéder à ce contenu gratuitement!
INSCRIPTION