Envoyez votre messageInfos
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Justifier qu’une suite n’est ni arithmétique, ni géométrique
Utilisation d’une suite auxiliaire arithmétique
Variations d’une suite
Limite d’une suite
Ressources associées et exercices semblables
Vidéo de l’exercice
On admet que $u_n\neq 4$ pour tout entier naturel $n$.
- Calculer $u_1$ et $u_2$.
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que $(u_n)$ n'est ni arithmétique, ni géométrique
Aide
On peut montrer que la différence puis le quotient de deux termes consécutifs n'est pas constante
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - Montrer que la suite $(v_n)$ est arithmétique.
Rappel cours
Suite arithmétique
Une suite $(u_n)$ est arithmétique s'il existe un réel $r$ tel que pour tout entier naturel $n$, $u_{n+1}=u_n+r$
$r$ est la raison de la suite.
On a alors $u_{n+1}-u_n=r$ donc la différence de deux termes consécutifs est constante et égale à $r$Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire l'expression de $v_n$ puis de $u_n$ en fonction de $n$
Rappel cours
Forme explicite d'une suite arithmétique
Si $(u_n)$ est arithmétique de raison $r$ est premier terme $u_0$, on a:
$u_n=u_0+nr$ et pour tous entiers $n$ et $p$, $u_n=u_p+(n-p)r$
Attention, si le premier terme de la suite est $u_1$ par exemple, on a alors $u_n=u_1+(n-1)r$Aide
Il faut calculer le premier terme de $(v_n)$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - En déduire les variations de $(u_n)$ et sa limite
Rappel cours
Étude des variations(différence de deux termes consécutifs)
Pour étudier les variations de $(u_n)$, il faut comparer $u_{n+1}$ et $u_n$.
Exprimer $u_{n+1}-u_n$ en fonction de $n$
Étudier le signe de l'expression obtenue
Si $u_{n+1}-u_n >0 $ alors$u_{n+1} >u_n$ et donc la suite $(u_n)$ est croissante.
Si $u_{n+1}-u_n <0 $ alors$u_{n+1} < u_n$ et donc la suite $(u_n)$ est décroissante. Limite d'un quotient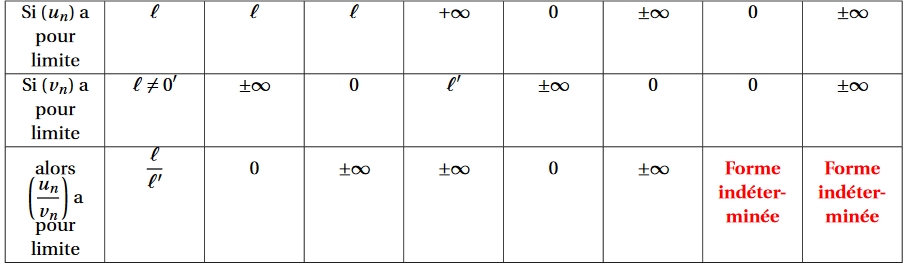
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements