contact@maths-lycee.fr
(+33) 07 59 58 68 37
MAHS-LYCEE
MATHS-LYCEE

AIDE EN LIGNE: un professeur à vos côtés

Bonjour,
L'aide en ligne est réservée aux abonnés PREMIUM.

Ressources et services proposés

Rejoignez-nous

Abonnements (free, basique et premium)

contact whatsapp Envoyez votre message
Vous pouvez aussi utiliser le formulaire de contact.

Planning aujourd'hui (Dimanche) : 10h00 à 23h00
Planning prévisionnel :
Lundi : 14h00 à 23h00
Mardi : 09h00 à 12h00 puis de 16h00 à 23h30

Home TERMINALE SPÉCIALITÉ MATHS Chapitre 7 géométrie dans l'espace Séquence 2 repérage dans l'espace et équation paramétrique d'une droite

Alignement dans un repère de l’espace, vecteurs coplanaires (réf 1253)

Ressource précédente: Vecteurs colinéaires et alignement dans un repère de l’espace (réf 1254) Ressource suivante: Équation paramétrique d’une droite (réf 1255)
Infos

Vous devez être inscrit pour accéder à ces informations.

Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.

Inscrivez vous gratuitement ici....

Contenu

Vecteurs colinéaires et alignement dans un repère de l’espace

Vecteurs coplanaires

Ressources associées et exercices semblables

Parallélogramme dans un repère de l’espace (réf 1252)
exercice

Vecteurs colinéaires et alignement dans un repère de l’espace (réf 1254)
exercice

Produit scalaire, équations de droites et de plans dans un repère de l’espace (réf 1298)
mémo

Exercice | temps recommandé entre 5 et 10mn | Niveau 1 application directe du cours | séquence 2 du chapitre |

Vidéo de l’exercice

L'espace est muni d'un repère $(O;\overrightarrow{i};\overrightarrow{j};\overrightarrow{k})$ et on donne les points $A(2;-3;1)$, $B(1;3;5)$ et $C(-1;3;-2)$.
  1. Calculer les coordonnées du vecteur $\overrightarrow{AB}$ puis du vecteur $\overrightarrow{AC}$.
    Rappel cours

    Coordonnées d'un vecteur dans l'espace
    L'espace est muni d'un repère quelconque.
    Soit $A(x_A;y_A;z_A)$ et $B(x_B;y_B;z_B)$
    $\overrightarrow{AB}\begin{pmatrix} x_B-x_A\\ y_B-y_A\\ z_B-z_A \end{pmatrix} $

    Solution

    Vous devez être abonné pour accéder à ce contenu...
    Infos abonnements

  2. Vérifier que les points $A$, $B$ et $C$ ne sont pas alignés.
    Aide

    $A$, $B$ et $C$ sont alignés si et seulement si les vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$ sont colinéaires.

    Solution

    Vous devez être abonné pour accéder à ce contenu...
    Infos abonnements

  3. Déterminer les coordonnées du point $M$ défini par la relation $\overrightarrow{AM}=2\overrightarrow{AB}-3\overrightarrow{AC}$
    Aide

    On a donc $x_{\overrightarrow{AM}}=2x_{\overrightarrow{AB}}-3x_{\overrightarrow{AC}}$

    Solution

    Vous devez être abonné pour accéder à ce contenu...
    Infos abonnements

  4. Que peut-on en déduire pour les points $A$, $B$, $C$ et $M$?
    Rappel cours

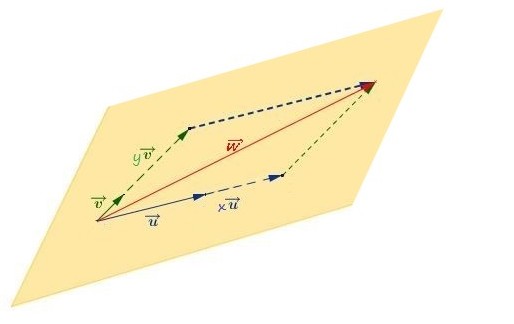
    vecteurs coplanaires
    Trois vecteurs $\overrightarrow{u}$, $\overrightarrow{v}$ et $\overrightarrow{w}$ non nuls sont coplanaires si les points $A$, $B$, $C$ et $D$ définis par $\overrightarrow{AB}=\overrightarrow{u}$, $\overrightarrow{AC}=\overrightarrow{v}$ et $\overrightarrow{AD} =\overrightarrow{w}$ sont dans un même plan.

    Solution

    Vous devez être abonné pour accéder à ce contenu...
    Infos abonnements

  5. On donne $N(5;y;z)$, déterminer les coordonnées de $N$ pour que $A$, $B$ et $N$ soient alignés.
    Aide

    Il faut que les vecteurs $\overrightarrow{AN}$ et $\overrightarrow{AB}$ soient colinéaires.

    Solution

    Vous devez être abonné pour accéder à ce contenu...
    Infos abonnements


Vidéo de l’exercice

Retour sur le corrigé
Vous devez être abonné pour accéder à ce contenu...

Infos abonnements

Ressource précédente: Vecteurs colinéaires et alignement dans un repère de l’espace (réf 1254) Ressource suivante: Équation paramétrique d’une droite (réf 1255)
This website uses cookies to improve your experience. If you continue to use this site, you agree with it.