Envoyez votre messageInformations
Vous devez être inscrit pour accéder à ces informations.
Ceci vous permet de visualiser les ressources déjà vues et marquer à revoir celles qui nécessitent d'être retravaillées.
Contenu
Lecture d’un tableau de variation:
Ensemble de définition
Représentation graphique de la fonction
Ressources associées et exercices semblables
compléter un tableau de variation et tracé de la courbe (réf 0210)
exercice
compléter un tableau de variation et tracé de la courbe (réf 0211)
exercice
Vidéo de l’exercice
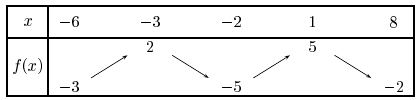
- Déterminer l'ensemble de définition $D_f$ de $f$.
Rappel cours
Ensemble de définition
L'ensemble de définition d'une fonction $f$ est l'ensemble des valeurs pour lesquelles on peut calculer l'image par $f$.
Par exemple, l'ensemble de définition de la fonction $f$ définie par $f(x)=\dfrac{1}{x+2}$ est $\mathbb{R}\setminus \lbrace -2\rbrace$ car le dénominateur doit être différent de $0$.Aide
La première ligne du tableau correspond aux valeurs prises par $x$
Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements - L'image de 0 par $f$ est 3.
Les antécédents de 0 par $f$ sont $-4$, $-2,5$, $-1$ et 4.
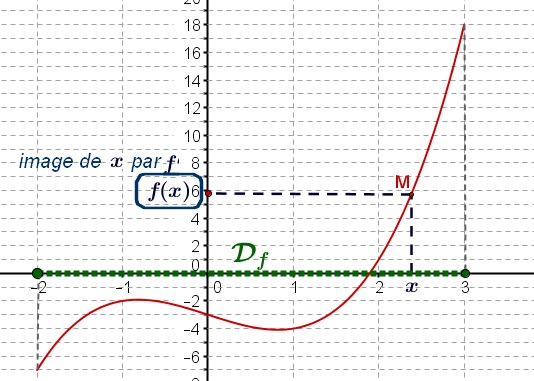
En utilisant le tableau de variation et les informations ci-dessus, donner une représentation graphique possible de $f$.Rappel cours
Représentation graphique
Soit $f$ une fonction définie sur un sous-ensemble $\mathcal{D}$ de $\mathbb{R}$.
La courbe représentative de $f$ est l'ensemble des points du plan (muni d'un repère) de coordonnées $(x;f(x))$ avec $x\in \mathcal{D}$.
Aide
Il faut placer les points dont les coordonnées sont données dans le tableau de variation.
On a aussi $f(-4)=0$, $f(-2,5)=0$...Solution
Vous devez être abonné pour accéder à ce contenu...
Infos abonnements